Дифференциальное уравнение волны

Получим дифференциальное уравнение волны; для этого найдём производные (4.46):

;

;

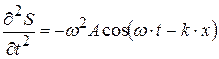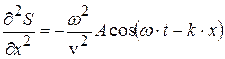откуда

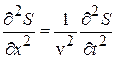. (4.50)

Это уравнение волны, распространяющейся вдоль оси OX. Более общее уравнение такое:

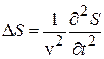, (4.51)

где 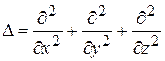– оператор Лапласа; 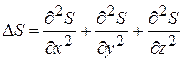. Волновому уравнению (4.51) удовлетворяет не только решение (4.46) – плоская волна, распространяющаяся вдоль положительного направления оси OX, но и (4.52) – волна бежит в отрицательном направлении оси OX; (4.53) – общий случай плоской волны; (4.54) – сферическая волна:

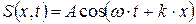; (4.52)

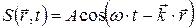; (4.53)

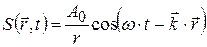. (4.54)