Скорость упругих волн.

Скорость продольных волн в упругой среде

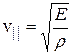; (4.59)

скорость поперечных волн в упругой среде

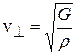; (4.60)

скорость распространения волн по натянутой струне

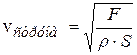. (4.61)

Здесь 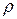– плотность, 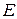– модуль Юнга, 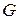– модуль сдвига, 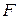– сила натяжения струны, 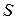– её сечение.

Найдём скорость звука в газе, исходя из (4.59). По закону Гука для упругой среды 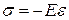. Здесь механическое напряжение можно интерпретировать как дополнительное давление, возникающее при распространении волны:

,

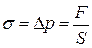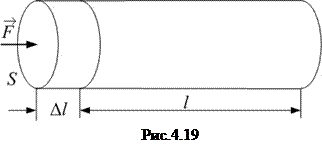а относительная деформация столба газа 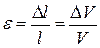(рис.4.19). Тогда

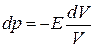. (4.62)

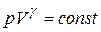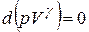
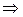
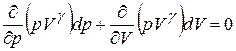
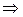
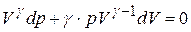
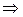
Процесс можно считать адиабатическим (при достаточно больших частотах звука), тогда состояние газа подчиняется уравнению Пуассона: . Полный дифференциал константы есть ноль, поэтому 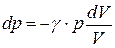. Сравнив с (4.62), получим:

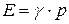. (4.63)

Из уравнения Менделеева-Клапейрона 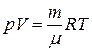получим выражение для плотности газа: 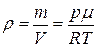. Подставим это выражение и (4.63) в (4.59):

.

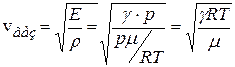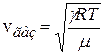. (4.64)