Стоячие волны.
 Пусть стержень длиной
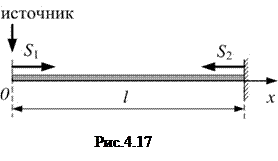
Пусть стержень длиной  закреплён у правого конца (
закреплён у правого конца ( 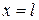 ). На левом конце (
). На левом конце ( 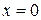 ) – источник упругих колебаний (рис.4.17), описываемых уравнением:
) – источник упругих колебаний (рис.4.17), описываемых уравнением:
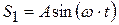 . (4.55)
. (4.55)
Волна, добежав до правого закреплённого конца стержня, отражается и бежит в обратном направлении, отставая по фазе от первичной на 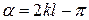 (
(  – путь волны по стержню и обратно;
– путь волны по стержню и обратно; 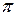 – потеря пол-длины волны при отражении):
– потеря пол-длины волны при отражении):
 . (4.55)
. (4.55)
Результирующая волна:
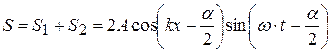 . (4.56)
. (4.56)
Переменные 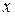 и
и 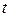 разделились
разделились 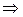 это стоячая волна. Она не переносит энергии. Все точки колеблются в одной фазе, только с различной амплитудой, зависящей от координаты
это стоячая волна. Она не переносит энергии. Все точки колеблются в одной фазе, только с различной амплитудой, зависящей от координаты 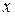 :
:
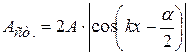 . (4.57)
. (4.57)
Найдём узлы стоячей волны, то есть точки, где амплитуда равна нулю:

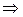
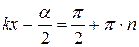 (
( 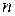 – целое)
– целое) 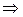
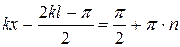
|
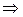
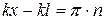
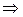
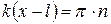
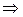
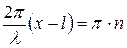
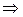
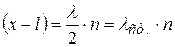 . (4.58)
. (4.58)
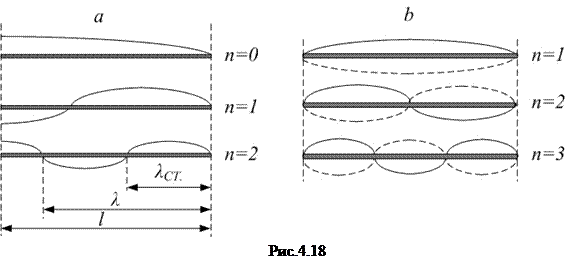
Выражение (4.58) означает, что узлы стоячей волны расположены на расстоянии, кратном длине стоячей волны 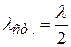 , от закреплённого конца стержня. Если второй конец свободен, там будет пучность (максимум) стоячей волны, и на длине стержня будет укладываться полуцелое число длин стоячих волн (рис.4.18, а):
, от закреплённого конца стержня. Если второй конец свободен, там будет пучность (максимум) стоячей волны, и на длине стержня будет укладываться полуцелое число длин стоячих волн (рис.4.18, а):
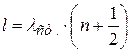 ;
;
а если второй конец закреплён, то целое (рис.4.18,b):
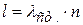 .
.
 |  |
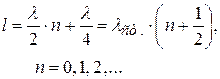
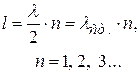
Дата добавления: 2015-04-10; просмотров: 1769;
