Энергия волны. Групповая скорость. Вектор плотности потока энергии (вектор Умова). Интенсивность волны
Энергия упругой волны 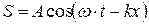 складывается из кинетической энергии колеблющихся частиц среды и потенциальной энергии упругой деформации:
складывается из кинетической энергии колеблющихся частиц среды и потенциальной энергии упругой деформации:
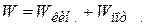 .
.
Для объёмной плотности энергии 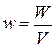 :
:
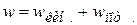 .
.
Объёмная плотности кинетической энергии равна
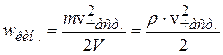 ,
,
где 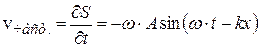 – скорость частиц среды. Тогда
– скорость частиц среды. Тогда
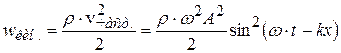 . (4.65)
. (4.65)
Оъёмную плотность потенциальной энергии упругой деформации можно выразить через модуль Юнга среды и относительную деформацию (рис.4.19):
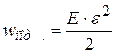 .
.
Относительную деформацию можно записать как
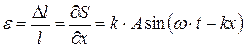 , тогда
, тогда
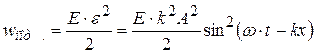 .
.
Из (4.59) модуль Юнга 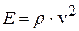 , а волновое число (волновой вектор)
, а волновое число (волновой вектор) 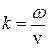 ; тогда
; тогда 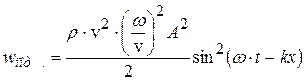 ;
;
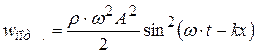 . (4.66)
. (4.66)
Сравнение (4.65) и (4.66) показывает, что 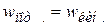 . Объёмная плотность полной энергии
. Объёмная плотность полной энергии
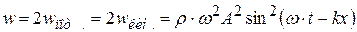 . (4.67)
. (4.67)
Точки с максимальным значением объёмной плотности энергии, равным 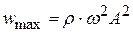 , перемещаются в пространстве со скоростью
, перемещаются в пространстве со скоростью 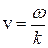 . Это – групповая скорость
. Это – групповая скорость 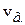 , то есть скорость переноса энергии. Или: групповая скорость – скорость перемещения точек, соответствующих максимальной плотности энергии. Для рассмотренной монохроматической волны она оказалась равной фазовой скорости.
, то есть скорость переноса энергии. Или: групповая скорость – скорость перемещения точек, соответствующих максимальной плотности энергии. Для рассмотренной монохроматической волны она оказалась равной фазовой скорости.
Если фазовая скорость волны зависит от частоты: 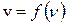 (диспергирующая среда), то
(диспергирующая среда), то 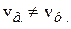 . Возможны случаи как
. Возможны случаи как 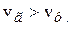 ,так и
,так и 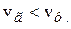 . Для электромагнитных волн возможно даже
. Для электромагнитных волн возможно даже 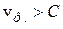 - скорости света в вакууме, поскольку фазовая скорость не связана с переносом энергии (или информации). Однако всегда
- скорости света в вакууме, поскольку фазовая скорость не связана с переносом энергии (или информации). Однако всегда 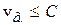 - нельзя передавать энергию или информацию быстрее скорости света в вакууме.
- нельзя передавать энергию или информацию быстрее скорости света в вакууме.
Групповая скорость – скорость перемещения центра волнового пакета (рис.4.20).
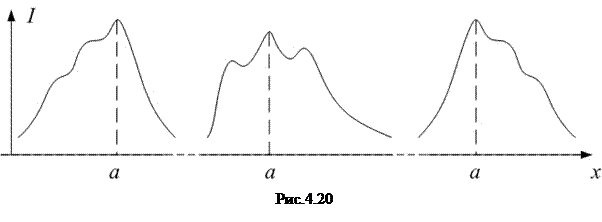 |
Волновой пакет – группа близких по волновым числам и по частотам монохроматических волн. Их амплитуды и фазы таковы, что в любой момент времени их сложение даёт ограниченный в пространстве одиночный импульс. Если нет дисперсии (
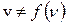 ), волновой пакет сохраняет свою форму в процессе распространения. При наличии дисперсии пакет деформируется: одни монохроматические составляющие распространяются быстрее, другие - медленнее. Групповая скорость – скорость перемещения точки a (см. рис.4.20) с максимальной плотностью энергии (максимальной амплитудой). В этой точке должны совпадать фазы всех монохроматических составляющих (условие максимума при наложении волн), то есть фаза не зависит от волнового числа:
), волновой пакет сохраняет свою форму в процессе распространения. При наличии дисперсии пакет деформируется: одни монохроматические составляющие распространяются быстрее, другие - медленнее. Групповая скорость – скорость перемещения точки a (см. рис.4.20) с максимальной плотностью энергии (максимальной амплитудой). В этой точке должны совпадать фазы всех монохроматических составляющих (условие максимума при наложении волн), то есть фаза не зависит от волнового числа:
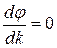 ;
; 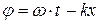
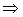
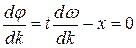
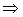
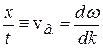 , в отличие от фазовой скорости, равной
, в отличие от фазовой скорости, равной 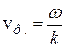 . Поскольку
. Поскольку 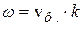 , то
, то
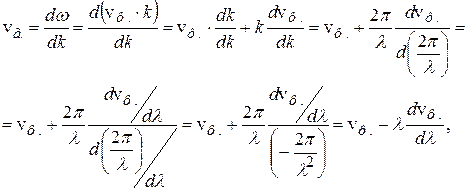
поскольку 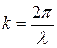 . Итак, групповая скорость связана с фазовой соотношением:
. Итак, групповая скорость связана с фазовой соотношением:
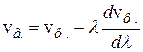 . (4.68)
. (4.68)
Дата добавления: 2015-04-10; просмотров: 1380;
