Основне рівняння квантової механіки - рівняння Шредінгера

Рівняння, що описує рух мікрочастинки, мас відтворю­вати її хвильові властивості, тобто повинне бути подібним до хвильового рівняння, що описує поширення оптичних або акустичних хвиль

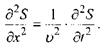(7.7)

Ми можемо міркувати таким чином: якщо мікро­частинка, яка рухається, має хвильові властивості і може бути охарактеризована довжиною хвилі, то її стан можна описати за допомогою деякої функції ЧУ, яка задовольняти­ме хвильове рівняння (7.7), тобто

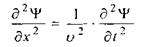(7.8)

Враховуючи зв'язок між частотою і періодом 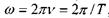, а також зв'язок між довжиною хвилі, швидкістю і періодом 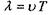і формулу для довжини хвилі де Бройля, відношення 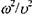можна подати таким чином:

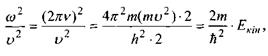(7.9)

Тоді рівняння набуває такий вигляд:

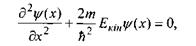(7.10)

де 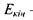- кінетична енергія частинки. Рівняння (7.10) описує одновимірний рух частинки. У випадку, коли частинка рухається в тривимірному просторі, рівняння (7.10) матиме вигляд:

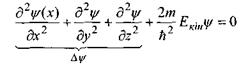(7.11)

або

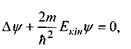(7.12)

де 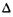- так званий оператор Лапласа, який діє на хвильову функцію і дорівнює сумі всіх других просторових похідних від 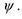Рівняння (7.12) описує рух вільної частинки.

Якщо частинка рухається в силовому полі, то її повна енергія дорівнює сумі кінетичної та потенціальної енергій: 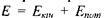, звідки 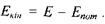У цьому випадку рівняння (7.12) записується таким чином:

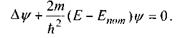(7.13)

Рівняння (7.13) - стаціонарне рівняння Шредінгера, запропоноване ним у 1926 році.