Співвідношення невизначеностей Гейзенберга
Хвильові властивості мікрочастинок свідчать про обмеженість застосування до них деяких понять, якими характеризуються тіла в класичній механіці. Так, в класичній механіці ми можемо одночасно вказати положення тіла в просторі та його імпульс, що дас змогу вказати просторове положення тіла у наступний момент часу, визначаючи тим самим траєкторію його руху. Для мікрочастинки це стає неможливим. Завжди існують невизначеності у значеннях її координати та імпульсу, пов'язані певним співвідношенням, яке було встановлено в 1927 р. німецьким фізиком В. Гейзенбергом:
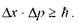 (7.5)
(7.5)
З цього співвідношення випливає, що чим точніше ми спробуємо визначити координату частинки, тим з меншою точністю зможемо охарактеризувати її імпульс:
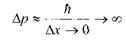
Приклад: згідно з класичним уявленням електрон в атомі рухається по коловій орбіті зі швидкістю 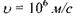 Цю швидкість легко визначити за умови . тобто
Цю швидкість легко визначити за умови . тобто 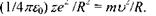
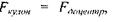
Належність електрона до атома потребує, щоб невизначеність у значенні його координати відповідала атомним розмірам, тобто 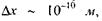 тоді із співвідношення
тоді із співвідношення 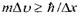 маємо
маємо
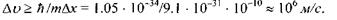
Звідси випливає, що невизначеність у значенні швидкості електрона дорівнює самій швидкості. Таким чином, неможливо зберегти уявлення про орбіту, вздовж якої рухається електрон з визначеною швидкістю, тобто класичні уявлення у даному випадку ми не в змозі застосувати.
Аналогічно пов'язані між собою невизначеності енергії частинки і часу її життя в даному енергетичному стані:
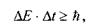 (7.6)
(7.6)
а також невизначеності моменту імпульсу та кутової координати.
Наведені співвідношення називаються співвідношеннями невшначеностей Гейзенберга. Вони становлять одне з основних положень квантової механіки. Відмова від детермінованого поняття траєкторії руху, притаманного класичній механіці Ньютона-Галілея, і перехід до ймовірносного опису положення мікрочастинок у просторі є однією з істотних і принципових особливостей квантової механіки — науки про мікросвіт.
Цікаво зазначити, що принцип невизначеностей зустрічається і в класичній фізиці, що має своє відображення у такому прикладі. Справді, із формули (7.6) випливає такий зв'язок між невизначеностями частоти 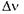 і часу вимірювання
і часу вимірювання 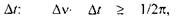 який повністю підтверджується медичною практикою. За малий проміжок часу
який повністю підтверджується медичною практикою. За малий проміжок часу 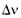 (скажімо,
(скажімо, 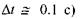 неможливо точно виміряти частоту серцевих скорочень, тобто невизначеність частоти Ду є дуже великою.
неможливо точно виміряти частоту серцевих скорочень, тобто невизначеність частоти Ду є дуже великою.
Дата добавления: 2015-06-22; просмотров: 1266;
