Основні співвідношення.
Із попереднього розділу слідує, що наявність деякої кількості точкових дефектів у твердих тілах пов’язано із присутністю домішок та інших зовнішніх факторів. Разом з тим кристалі певна кількість точкових дефектів виникає внаслідок теплового руху. Внаслідок цього ентропія системи повинна зрости. Тому при аналізу процесів виникнення точкових дефектів у кристалах, як правило, виходять із балансу складових ентропійної та вільної енергії - внутрішньої енергії, яка при наявності деякої кількості точкових дефектів може дещо зрости, тобто
 ,
,
де U- внутрішня енергія, T- абсолютна температура, S - ентропія.
При утворенні точкових дефектів може змінитися і об’єм системи V. В цьому випадку необхідно виходити із термодинамічного потенціалу
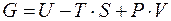 (2.1)
(2.1)
Виходячи із умови мінімуму G при зміні концентрації n дефектів можна визначити рівноважну їх концентрацію при даній температурі.
Розглянемо випадок двохкомпонентної системи, що складається із часток 1-го та 2-го сорту, а також вважатимемо, що дана система складається із двох підграток, що відповідають двом сортам структурних елементів. Відповідно до цього приймемо наступні позначення:
 і
і 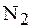 - повне число вузлів в підграnці- 1 та 2;
- повне число вузлів в підграnці- 1 та 2;
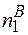 і
і 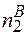 - число вакантних вузлів в підгратках 1 і 2;
- число вакантних вузлів в підгратках 1 і 2;
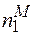 і
і 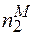 - число часток відповідно першого та другого сорту, що знаходяться в міжвузлях своїх граток;
- число часток відповідно першого та другого сорту, що знаходяться в міжвузлях своїх граток;
 і
і 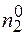 - число часток першого та другого сорту, які знаходяться відповідно у вузлах другої та першої підграток;
- число часток першого та другого сорту, які знаходяться відповідно у вузлах другої та першої підграток;
N0 - число міжвузольних позицій.
Очевидно, що різниця 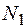 -
- 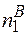 -
- 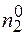 відповідає числу частинок 1- го сорту, які залишились на своїх місцях у підгратці 1, в той же час
відповідає числу частинок 1- го сорту, які залишились на своїх місцях у підгратці 1, в той же час
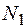 -
- 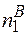 -
- 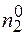 +
+ 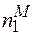 +
+  =
=  (2.2)
(2.2)
є загальне число часток 1-го сорту. Аналогічно
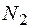 -
- 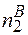 -
-  +
+ 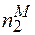 +
+ 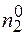 =
= 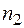 (2.3)
(2.3)
Загальне число часток 2-го сорту. Відношення
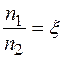 (2.4)
(2.4)
буде характеризувати ступінь стехіометрії. В загальному випадку 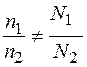 , тобто кристали можна вважати не стехіометричними.
, тобто кристали можна вважати не стехіометричними.
Величина 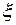 є параметром, який визначається способом вирощування кристалу, обробки і т.д. Із співвідношення (2.4) також слідує, що не всі
є параметром, який визначається способом вирощування кристалу, обробки і т.д. Із співвідношення (2.4) також слідує, що не всі  є незалежними змінними.
є незалежними змінними.
У сучасній теорії розупорядкування допускається, що 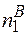 ,
, 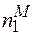 ,
,  <<
<< 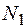 і
і 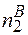 ,
, 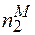 ,
, 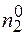 <<
<< 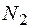 . З іншої сторони це значить, що
. З іншої сторони це значить, що
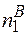 ,
, 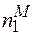 ,
,  <<
<< 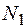 -
- 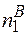 -
- 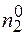
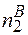 ,
, 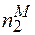 ,
, 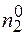 <<
<< 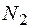 -
- 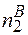 -
-  ,
,
тобто число розупорядкованих часток даного сорту мале в порівнянні з нерозупорядкованими частками того ж сорту, які знаходяться в нормальних вузлах гратки. Іншими словами випадки безпосереднього сусідства дефектів любого типу між собою повинні бути рідкі. Тому енергією взаємодії дефектів між собою можна знехтувати. При такому допущенні вклади систем дефектів різного типу можна вважати адитивними. Наприклад, внутрішню енергію можна виразити у вигляді лінійної функції дефектів різної природи:
 . (2.5)
. (2.5)
Тут  значить енергію ідеального кристалу, яка припадає на одну структурну одиницю в ідеальному кристалі, складеному із
значить енергію ідеального кристалу, яка припадає на одну структурну одиницю в ідеальному кристалі, складеному із 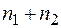 елементів, а
елементів, а  - число структурних одиниць із яких складений даний кристал. Наприклад, для стехіометричного кристалу типу AB
- число структурних одиниць із яких складений даний кристал. Наприклад, для стехіометричного кристалу типу AB  співпадає з
співпадає з  . У випадку кристалу
. У випадку кристалу 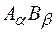 , де a< b, число n =
, де a< b, число n = 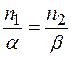 .
.
У випадку не стехіометричних кристалів, наприклад кристалу із надлишком B - компоненти 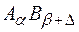
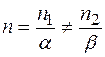 . При цьому слід зауважити, що для нестехіометричних кристалів в праву частину виразу для U слід добавити складову, яка відображає той факт, що введення в кристал надлишкової В - компоненти одночасно значить формування в першій підгратці деякої кількості вакансій
. При цьому слід зауважити, що для нестехіометричних кристалів в праву частину виразу для U слід добавити складову, яка відображає той факт, що введення в кристал надлишкової В - компоненти одночасно значить формування в першій підгратці деякої кількості вакансій 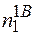 , рівній надлишку компоненти В. У співвідношенні (2.5)
, рівній надлишку компоненти В. У співвідношенні (2.5) 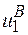 значить зміну енергії при переході частинки сорту “1” із вузла підгратки “1” на безмежність;
значить зміну енергії при переході частинки сорту “1” із вузла підгратки “1” на безмежність; 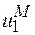 - приріст енергії при втіленні частинки “2” із безмежності у вузол підгратки “2”;
- приріст енергії при втіленні частинки “2” із безмежності у вузол підгратки “2”; 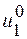 - зміна енергії при віддаленні частки “2” із вузла підгратки “2” на безмежність і заміні її часткою сорту “1” із безмежності. Значення інших символів аналогічні.
- зміна енергії при віддаленні частки “2” із вузла підгратки “2” на безмежність і заміні її часткою сорту “1” із безмежності. Значення інших символів аналогічні.
Подібним же чином можна описати зміну об’єму системи в кристалі з дефектами.
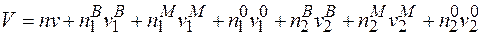 . (2.6)
. (2.6)
Найбільший інтерес представлятиме співвідношення для ентропії в (2.1). Нам уже відомо, що в загальному випадку ентропія системи може бути розділена на дві частини - ентропія, що пов’язана із внутрішніми степенями вільності, зумовленої тепловим рухом  і конфігураційної ентропії.
і конфігураційної ентропії.  , всі інші ентропійні зміни, що пов’язані із особливостями коливання гратки поблизу точкових дефектів, відомі і характеризуються параметрами
, всі інші ентропійні зміни, що пов’язані із особливостями коливання гратки поблизу точкових дефектів, відомі і характеризуються параметрами  . Тоді
. Тоді
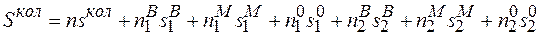 . (2.7)
. (2.7)
Для конфігураційної складової, як нам уже відомо
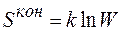 .
.
Для того, щоб знайти W, згадаємо, що із N різних елементів можна скласти реалізувати N! перестановок, які різняться одна від другої тільки порядком входячих в них елементів. Якщо серед цих N елементів є однакові, то частина перестановок нерозрізнима між собою і число різних перестановок зменшиться. Допустимо, що один елемент повторюється a, другий b, а третій g раз і т.д. Тоді число різних перестановок
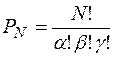 (2.8)
(2.8)
У нашому випадку всі структурні елементи, що знаходяться у вузлах підграток, всі вакансії, втілені в міжвузольні положення атоми та інші дефекти фізично не відрізняються один від одного. Тоді користуючись формулою (2.8), запишемо:
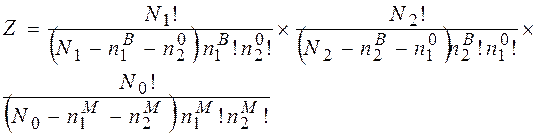 (2.9)
(2.9)
Добуток цих співмножників береться так, щоб для кожної конфігурації ’’2’’ або ’’0’’ можна було здійснити весь перебір конфігурацій ’’1’’ і т.д. Використовуючи формулу Стірлінга

яка при дуже великих N приймає вид
 .
.
Тоді, наприклад, перша складова (2.9) перетвориться до виду


Перетворимо першу складову до виду
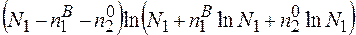
і групуючи доданки з одинаковими передлогарифмічними множниками, отримаємо
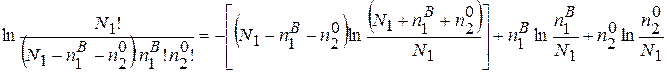
Розклавши таким же чином і інші складові та згрупувавши їх з однаковими перед логарифмічними множниками, матимемо
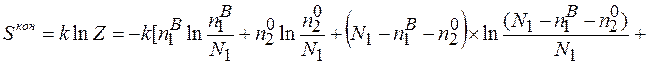
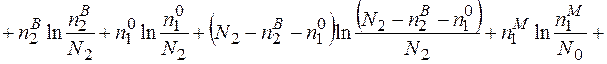
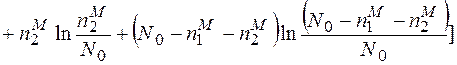 (2.10)
(2.10)
Підставивши співвідношення (2.10), (2.5), (2.6), (2.7), в (2.1) отримаємо
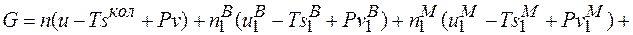

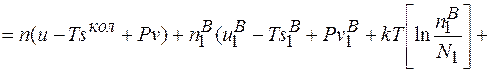
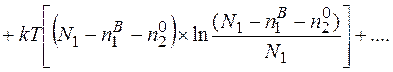 (2.11)
(2.11)
Отже, для розв’язку задачі необхідно знайти варіацію (2.11):
 (2.12)
(2.12)
Система рівнянь (2.12) визначає рівноважні значення: 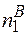 ,
, 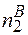 ,
, 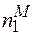 ,
, 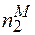 ,
,  ,
, 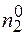 .
.
При цьому слід мати на увазі, що в силу (2.4) та інших умов не всі змінні є незалежними. Тому рівність нулю варіації (2.12), ще не значить, що  . Рівність нулю похідних
. Рівність нулю похідних  може бути умовою рівноваги тільки в деяких часткових випадках.
може бути умовою рівноваги тільки в деяких часткових випадках.
Зауважимо, що потенціал G є функцією таких параметрів системи - P і T, які при адитивному сумуванні двох систем не залежать від числа часток. Тому потенціал G є єдиним потенціалом, який зручно представити у вигляді
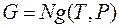 ,
,
де N - число часток, які складають термодинамічну систему.
У випадку системи із однакових часток функцію g(P,T) можна розглядати, як потенціал в розрахунку на одну частку. Із термодинаміки із змінним числом часток відомо, що похідні  представляють собою хімічні потенціали. Тому
представляють собою хімічні потенціали. Тому

Тоді повертаючись до (2.11), можна показати, що вираз
 (2.13)
(2.13)
повинен виражати хімічний потенціал досконалого кристалу.
В якості прикладу, проведемо деякі розрахунки

Отриманий вираз представляє собою зміну хімічного потенціалу 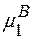 системи при формуванні вакансій в підгратці ’’1’’ за вирахуванням конфігураційної ентропії. Тоді можемо записати, що
системи при формуванні вакансій в підгратці ’’1’’ за вирахуванням конфігураційної ентропії. Тоді можемо записати, що 
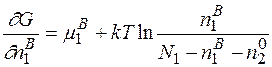 ,
,
оскільки  <<N1 і
<<N1 і 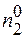 <<N1, то
<<N1, то
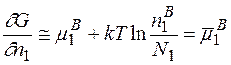 .
.
Таким же чином можна показати, що
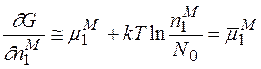
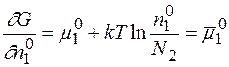 .
.
Нарешті отримаємо, що
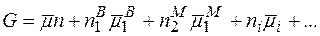 (2.14)
(2.14)
Контрольні питання
1. Які складові вільної енергії забезпечують енергетичний баланс кристалу, що містить точкові дефекти?
2. Пояснити фізичний зміст термодинамічного потенціалу кристалу.
3. Пояснити хід і умови утворення точкових дефектів у двокомпонентних кристалах.
4. Записати вирази для опису зміни внутрішньої енергії, об’єму та ентропії від концентрацій точкових дефектів у кристалі.
5. Описати зміну хімічного потенціалу від концентрації точкових дефектів
Дата добавления: 2015-06-10; просмотров: 802;
