Розупорядкування в двохкомпонентній системі.
Розгляд розупорядкування в двохкомпонентній системі значно ускладнюється, тому аналіз таких систем будемо проводити при таких припущеннях. Вважатимемо, що в системі обмінне розупорядкування відсутнє і що число вузлів підгратки “1” рівне числу вузлів підгратки “2”, тобто
N1 =N2 = N (2.18)
Подібна ситуація характерна для іонних кристалів, в яких безумовною вимогою є їх електронейтральність, тобто N1 - 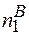 +
+ 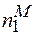 =N2 -
=N2 - 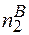 +
+ 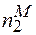 . Використовуючи (2.18) :
. Використовуючи (2.18) :
N - 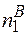 +
+ 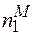 =N -
=N - 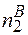 +
+ 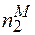 , або
, або 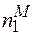 -
- 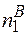 =
= 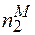 -
- 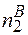 ,
,
причому не обов’язково, що 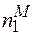 =
= 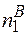 та
та 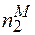 =
= 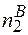
У загальному випадку існуючі в кристалі вакансії можна розділити на дві групи. Одні зв’язані з дефектами за Шоткі, а інші зобов’язані своїм походженням дефектам за Френкелем. Тому можна записати
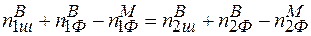 (2.19)
(2.19)
Причому 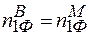 і
і 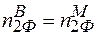 . Тоді із (2.19) слідує, що
. Тоді із (2.19) слідує, що
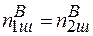 (2.20)
(2.20)
Отже, число дефектів за Шоткі аніонного і катіонного типу повинно бути однаковим, тобто дефекти за Шоткі в іонних кристалах повинні породжуватись парами. Це результат дуже важливий, оскільки він накладає певні умови на можливість народження точкових дефектів при різних процесах у кристалах.
Умова (2.20) фактично значить, що для забезпечення можливості добудови кристалу необхідні будівельні матеріали (елементи) всіх сортів, із яких складається даний кристал. З іншої сторони, як уже зазначалось, 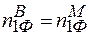 і
і 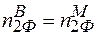 , тобто
, тобто 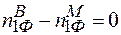 і
і 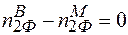 . Значить співвідношення (2.19) не накладає ніяких умов на кількість дефектів за Френкелем сорту “1” і “2”. Кількість дефектів за Френкелем в системі “1” –“2” може бути різним:
. Значить співвідношення (2.19) не накладає ніяких умов на кількість дефектів за Френкелем сорту “1” і “2”. Кількість дефектів за Френкелем в системі “1” –“2” може бути різним:
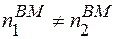 .
.
Тому число вакансій першого і другого сортів може бути різним.
Контрольні питання
1. Пояснити мови і механізми утворення точкових дефектів у двокомпонентному кристалі.
2. Яка принципова відмінність в утворенні точкових дефектів за Шоткі і Френкелем у одно- двокомпонентному кристалах?
3. Чому число дефектів за Шоткі аніонного і катіонного типу повинно бути однаковим?
4. Які умови накладаються на кількість дефектів за Френкелем?
§2.4. Дефекти за Шоткі в однокомпонентній системі.
Розглянемо випадок однокомпонентної системи, в якій можуть бути тільки дефекти за Шоткі, коли атом при формуванні вакансії вибуває із системи. Для такого випадку матимемо
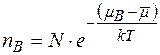 ,
,
де 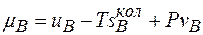 і
і 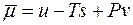 . Значить
. Значить
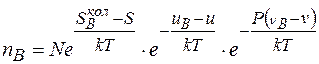 (2.21)
(2.21)
На жаль, як вже відзначалось раніше, точний розрахунок величин s, 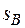 , u,
, u, 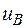 , v,
, v, 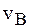 має значні труднощі. Тому допускається ряд спрощень. Вважається зовнішній тиск досить малим. Точний розрахунок коливної ентропії пов’язаний із розрахунком фононного спектру реальних кристалів.
має значні труднощі. Тому допускається ряд спрощень. Вважається зовнішній тиск досить малим. Точний розрахунок коливної ентропії пов’язаний із розрахунком фононного спектру реальних кристалів.
В ейнштейнівській моделі твердого тіла елементів у вузлах гратки атоми розглядаються як незалежні гармонічні осцилятори, що коливаються з однаковою частотою w. Відомо, що ентропія, пов’язана з цими коливаннями співвідношенням
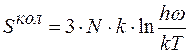 ,
,
де 3N - число степеней вільності 3N осциляторів.
Припустимо тепер, що в гратці є вакансія. Це значить, що поблизу дефектів частота коливань атомів повинна дещо змінитися, оскільки змінюються сили зв’язку. Наприклад, для вакансії повинно мати місце зменшення частоти. В цьому випадку
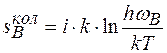 ,
,
де і - число ступенів вільностей, для яких змінилась частота коливань в результаті утворення дефекту. Очевидно і повинно бути порядку першого координаційного числа. Зміну ентропії можна виразити як
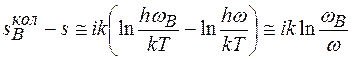 (2.22)
(2.22)
Зауважимо, що у випадку утворення дефекта за Френкелем зміна коливної ентропії менша, оскільки вакансія і втілений атом викликають зміну частоти в протилежних напрямках. Тоді підставляючи (2.22) в (2.21) отримаємо
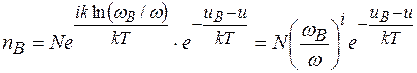 (2.23)
(2.23)
Другий множник в (2.21) представлений досить не зручно із-за того, що явно не виділена залежність від температури, а ефект теплового розширення обумовлений ангармонізмом коливань. Відомо, що
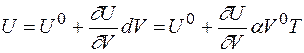 ,
,
a - коефіцієнт теплового розширення, V0- об’єм при T= 0°К, а U0- енергія при T=0°К. Тоді
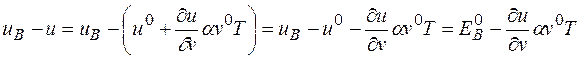 ,
,
де 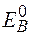 - енергія досконалого кристалу, що припадає на одну структурну одиницю, плюс енергія, яка зв’язана з утворенням вакансії при абсолютному нулі температури. Отримаємо
- енергія досконалого кристалу, що припадає на одну структурну одиницю, плюс енергія, яка зв’язана з утворенням вакансії при абсолютному нулі температури. Отримаємо
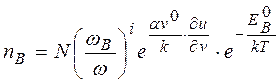 (2.24)
(2.24)
Контрольні питання
1. Записати вираз для знаходження концентрації точкових дефектів в однокомпонентних кристалах.
2. Від яких фізичних параметрів залежить концентрація точкових дефектів за Шоткі?
3. Чи змінюється частота коливань атомів у гратці?
4. Оцінити концентрацію дефектів за Шоткі в кремнії при Т=300 К і 1000 К за співвідношенням (2.24)
§2.5. Знаходження енергії розупорядкування.
2.5.1. Іонні кристали. Розглянемо спочатку випадок іонних кристалів. Для іонних кристалів енергія зв’язку підраховується достатньо просто:
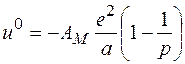 , (2.25)
, (2.25)
де 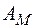 - постійна Маделунга, для кристалів із структурою типу NaCl
- постійна Маделунга, для кристалів із структурою типу NaCl 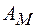 =1.746, а - постійна гратки; 1/р - враховує енергію відштовхування для галогенідів лужних металів р@9. Для іонних кристалів врахування додаткових змін внутрішньої енергії суттєве. По-скільки іони у вузлах гратки жорстко не закріплені, то при утворенні вакансії в її околі вони повинні зміщуватись так, що повинна мати місце поляризація зміщення, а також деформація електронних оболонок самих іонів - поляризація іонів.
=1.746, а - постійна гратки; 1/р - враховує енергію відштовхування для галогенідів лужних металів р@9. Для іонних кристалів врахування додаткових змін внутрішньої енергії суттєве. По-скільки іони у вузлах гратки жорстко не закріплені, то при утворенні вакансії в її околі вони повинні зміщуватись так, що повинна мати місце поляризація зміщення, а також деформація електронних оболонок самих іонів - поляризація іонів.
Для зручності кристал апроксимується континуальним діелектриком і діелектричною проникливістю e, а вакансія уподобляється наявністю в цьому діелектричному континуумі сферичної порожнини радіуса x. Поскільки, як уже підкреслювалось раніше, вакансія в іонних кристалах несе ефективний заряд, рівний оберненому заряду віддаленого іона. Тому в центр порожнини необхідно помістити заряд е. Наявність якого виключить поляризацію діелектрика. Тоді електричне зміщення 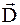 і напруженість поля
і напруженість поля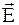 рівні:
рівні:
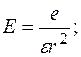
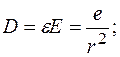
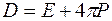 ,
,
а поляризація
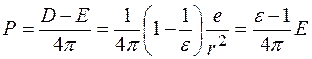
Потенціал в центрі сферичної порожнини, обумовлений цією поляризацією матиме вид
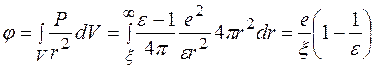
Отже, робота, яка необхідна для віддалення іона на безмежність рівна
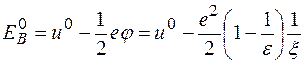 . (2.26)
. (2.26)
Множник 1/2 - тут тому, що по мірі віддалення іона поляризація поступово наростає від 0 до свого максимального значення. Недоліки даної моделі очевидні. Вони появляються при заміні діелектричного середовища континуумом і неможливістю точно визначити параметр x . Можна вважати, що x~а. Проведемо деякі оцінки. Якщо e~5 , а x~а, то
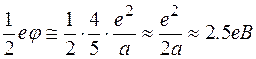 . (2.27)
. (2.27)
Оцінки дещо покращуються, якщо x - рівне радіусу іона для відповідної вакансії. Енергія зв’язку U0 для іонних кристалів складає ~ 6- 8еВ. Тому 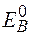 ~4-5еВ. Найбільш точні останні комп’ютерні розрахунки показали, що дана найпростіша модель дає найбільш правильні значення
~4-5еВ. Найбільш точні останні комп’ютерні розрахунки показали, що дана найпростіша модель дає найбільш правильні значення 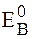 для x=0.9а для аніонної вакансії і x=0.6а- для катіонної.
для x=0.9а для аніонної вакансії і x=0.6а- для катіонної.
Наприклад: для NaCl енергія утворення катіонної вакансії 4,62еВ, а аніонної- 5,18еВ; для KCl – 4,47eB i 4,79eB; для KBr – 4,23eB i 4,60eB, відповідно.
2.5.2. Металічні кристали. Енергія утворення вакансії рівна енергії, яка потрібна, щоб віддалити атом із середини кристала на безмежність, а потім знову повернути його на поверхню. Досить приблизно цю енергію можна підрахувати, якщо базуватись тільки на енергії парних взаємодій. Якщо врахувати взаємодію тільки найближчих сусідів, то для віддалення атома на ¥ необхідно розірвати і зв’язків, а значить затратити енергію
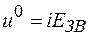
де 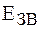 - енергія, що припадає на один зв’язок. При поверненні атома на поверхню реставрується і/m зв’язків. Таким чином, при утворенні дефекту за Шоткі тратиться робота:
- енергія, що припадає на один зв’язок. При поверненні атома на поверхню реставрується і/m зв’язків. Таким чином, при утворенні дефекту за Шоткі тратиться робота: 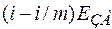 . Енергія
. Енергія 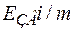 - це по суті енергія сублімації. Поскільки m=2, то для віддалення атома на безмежність тратиться подвоєна енергія сублімації (~3.6еВ). Цей результат є дещо завищеним, оскільки не враховуються релаксації за рахунок електронів і атомів навколо вакансії. Тому, як і для іонних кристалів
- це по суті енергія сублімації. Поскільки m=2, то для віддалення атома на безмежність тратиться подвоєна енергія сублімації (~3.6еВ). Цей результат є дещо завищеним, оскільки не враховуються релаксації за рахунок електронів і атомів навколо вакансії. Тому, як і для іонних кристалів
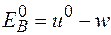 , (2.28)
, (2.28)
де w - енергія релаксації. Розглянемо із чого складається величина w (див. також параграф 2.8). Вона визначається зміною енергії взаємодії електронів з додатнім іоном при віддаленні останнього; власної енергії розподіленого заряду електронів; енергії відштовхування, яка викликана віддаленням іона і перерозподілом атомів навколо дефектів.
Базуючись на цих припущеннях Хантингтон і Зейц виконали розрахунки для міді [9]. Зауважимо, що цей метод розрахунку досить проблематично використати для інших металів. Тому існує досить спрощений метод, що грунтується на наступних припущеннях. Оскільки в процесі формування вакансії обриваються зв’язки, то електронний газ, який володіє високою рухливістю буде прагнути наситити ці зв’язки, зменшуючи тим самим енергію системи. Кількісно цей ефект еквівалентний тому випадку, коли б навколо вакансії формувалась вільна поверхня з деякою поверхневою енергією 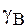 . Таким чином, всі зміни стану електронного газу зводяться до врахування деякої поверхневої енергії
. Таким чином, всі зміни стану електронного газу зводяться до врахування деякої поверхневої енергії 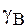 . Зміна енергії відштовхування і іонного остову може бути врахована в рамках моделі пружного континууму. Допустимо, що радіус іона r, якщо його забрати, то утворюється сферична порожнина, яка має деяку поверхневу енергію
. Зміна енергії відштовхування і іонного остову може бути врахована в рамках моделі пружного континууму. Допустимо, що радіус іона r, якщо його забрати, то утворюється сферична порожнина, яка має деяку поверхневу енергію
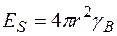 .
.
Після забирання іону відбувається пружна релаксація гратки, яка змінює r на величину er, де e- пружна деформація. Із теорії пружності відомо, що якщо сферична порожнина змінює свій радіус на величину er, то це пов’язано з пружною енергією
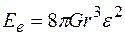 ,
,
де G - модуль зсуву.
Отже, при стиску гратки за рахунок пружної релаксації відбувається зміна r і змінюється поверхнева енергія на величину:
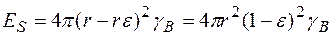 . (2.29)
. (2.29)
В результаті повна енергія
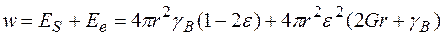 .
.
Якщо знайдемо розв’язок рівняння 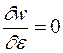 , то визначимо стан, який відповідає мінімуму енергії системи, тобто
, то визначимо стан, який відповідає мінімуму енергії системи, тобто
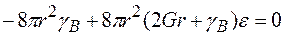 .
.
Звідси 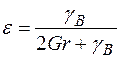 і
і
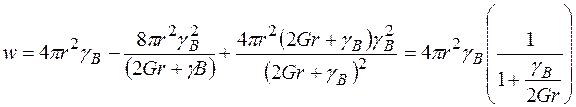 (2.30)
(2.30)
Отже, для вирахування енергії утворення дефекту необхідно знати величину поверхневої енергії. Величина поверхневої енергії g для металів відома. Проте вона відноситься для плоскої поверхні, в той же час як поверхня, після того як забраний атом, володіє значною кривизною. Із фізичних міркувань поверхнева енергія повинна бути пропорційна числу обірваних зв’язків , що припадають на одиницю поверхні. Тому можна записати
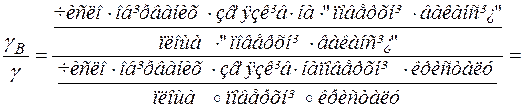

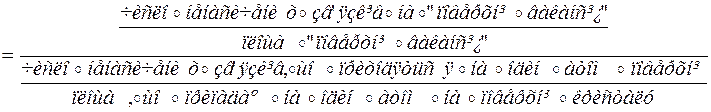 Якщо і - парне координаційне число, то число ненасичених зв’язків, що припадають на один атом на поверхні, рівне і/m, а на поверхні вакансії –і, отримаємо:
Якщо і - парне координаційне число, то число ненасичених зв’язків, що припадають на один атом на поверхні, рівне і/m, а на поверхні вакансії –і, отримаємо:
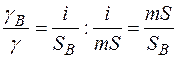 , (2.31)
, (2.31)
де S - площа, яка припадає на один атом поверхні, а 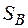 - поверхня багатогранника, що складається із атомів першої координаційної сфери. Для ГЦК- металів нескладно отримати наступні оцінки -
- поверхня багатогранника, що складається із атомів першої координаційної сфери. Для ГЦК- металів нескладно отримати наступні оцінки - 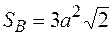 ,
, 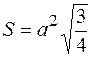 , m=4. Значить -
, m=4. Значить - 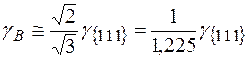 . На прикладі міді отримаємо -
. На прикладі міді отримаємо - 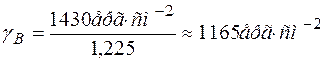 . Оскільки
. Оскільки 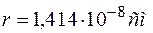 ,
, 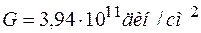 , тоді
, тоді 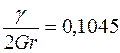 ,
, 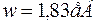 . Повна енергія зв’язку
. Повна енергія зв’язку 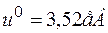 [9]. Отже, базуючись на вище приведених даних отримаємо
[9]. Отже, базуючись на вище приведених даних отримаємо
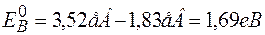
Більш строгі розрахунки провели Хантінгтон і Зейтц, їх значення енергії утворення вакансії в міді 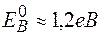 [9].
[9].
Контрольні питання
1. Записати вираз для розрахунку концентрації точкових дефектів за Шоткі в іонних кристалах.
2. Яку модель утворення вакансій використовують для розрахунку енергії утворення і їх концентрацій?
3. Які недоліки містить модель представлення вакансії у вигляді сферичної порожнини в діелектричному континуумі?
4. Від яких фізичних параметрів залежить енергія утворення вакансії в металічних кристалах?
5. Дати пояснення терміну «енергія релаксації» та її фізичний зміст.
6. Яка величина енергії утворення вакансії в ГЦК іонних кристалах?
7. Яка величина енергії утворення вакансії в міді?
§ 2.6. Конфігурації утворення дефектів за Френкелем у ГЦК -гратці
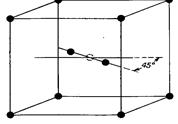
У випадку утворення дефектів за Френкелем ситуація виявляється більш складною. Це зв'язано з тим, що для впроваджуваних у гратку атомів у принципі можливе формування декількох міжвузольних станів. Наприклад, для впровадженого атома в ГЦК - гратках можливі три різні конфігурації, показані на рис.2.1- рис.2.2.
На жаль, метод розрахунку, викладений у попередньому параграфі, виявляється малопридатним, оскільки лінійна теорія пружності не може бути використана для опису спотворень гратки поблизу втіленого атома. Для розрахунку енергії утворення дефектів за Френкелем Хантінгтон і Зейтц застосували запропонований ними метод і знайшли, що енергія утворення міжвузольних атомів у міді складає ~5 - 6 еВ, тобто значно більше, ніж для дефектів за Шоткі. Відомі декілька можливих конфігурацій утворення міжвузольного дефекту, зокрема:
1) об’ємно - центрована (рис.2.1а);
2) розщеплена (рис.2.1б);
3) конфігурація краудіона (рис.2.2)
Остання конфігурація представляє собою міжвузольний атом, локалізований вздовж напрямку щільної упаковки так, що зміщення атомів із рівновіддалених положень лінійно спадають по мірі віддалення від центра спотворення, а рух краудіона може відбуватися тільки вздовж напрямку атомного ряду.
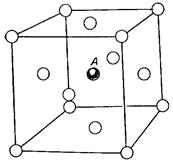
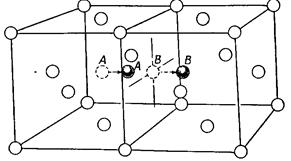
Рис.2.1. Дві конфігурації міжвузольного атому в ГЦК гратці: а - міжвузольний атом А в об’ємноцентрованій конфігурації; б - міжвузольний атом у розщепленій конфігурації: два атоми А і В ділять між собою вакантну атомну позицію, відстань між атомами є порядку 0.6×а (а - постійна гратки)

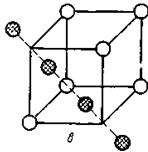
а) б)
Рис.2.2. Конфігурація міжвузольного атому в ГЦК гратці -— краудіон.
Розрахунки показали, що розщеплена конфігурація є більш стійкою, ніж об’ємноцентрована, а краудіона конфігурація є ще менш стійкою. Можливість існування розщепленої конфігурації френкелівського дефекту була підтверджена розрахунками на ЕОМ [8, 9]. При цьому, різниця в енергіях утворення об’ємно - центрованої і розщепленої конфігураціях порядку 0.1еВ.
Контрольні питання
1. Які можливі схеми утворення міжвузольних атомів в кристалах?
2. Яка енергія утворення точкових дефектів за Френкелем?
3. Які труднощі виникають при розрахунку енергії утворення дефектів за Френкелем?
Дата добавления: 2015-06-10; просмотров: 827;
