Термофлуктуаційні дефекти

Якщо температуру ідеального (бездефектного) кристала підвищити від абсолютного нуля до деякого значення Т >0, то в ньому виникнуть власні дефекти. Цей процес простіше представити з використанням конфігураційної діаграми (рис. 1.8). Остання є залежністю потенціальної енергії U деякої області кристала від узагальненої координати Q, роль якої, зокрема, може грати відстань між двома сусідніми атомами в гратках. Абсолютний мінімум на кривій U(Q) при Q = Q₀ відповідає рівноважному положенню обох атомів у вузлах гратки, а мінімум при Q = Q₁ – зсуву одного з атомів в найближче міжвузловинне положення. Таким чином, термофлуктуаційне утворення дефекту пов'язане з випадковими флуктуаціями амплітуди теплових коливань атомів на деякій мікроскопічній ділянці кристалу при досягненні максимуму на кривій U(Q).

Виникнення точкових дефектів приводить до збільшення внутрішньої енергії кристалу, оскільки для їх утворення необхідно затратити деяку кількість роботи.

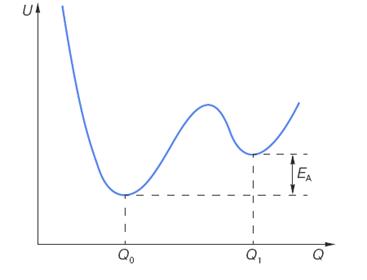
Рис. 1.8.Конфігураційна діаграма, яка пояснює термофлуктуаційний механізм утворення точкових дефектів. Q₀ і Q₁ відповідають регулярному і дефектному станам атомної конфігурації

Конфігураційна ентропія (ентропія зміщення) при цьому також збільшується, оскільки точкові дефекти можуть розміщуватися по вузлам гратки різними способами.

При Т>0 ⁰К вільна енергія може бути мінімальною при деякій концентрації точкових дефектів, яку можна визначити із балансу енергетичної та ентропійної складових. У гратці із N вузлами n дефектів можуть розміститися наступним числом способів:

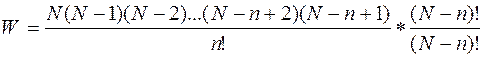
тобто

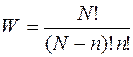
Як відомо, конфігураційна ентропія визначається виразом:

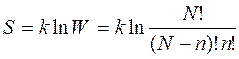(1.3)

Для спрощення виразу (1.3) використаємо формулу Стірлінга, тобто: ,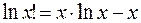

тоді вираз (1.3) можна переписати:

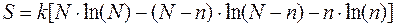
Якщо енергія утворення одного дефекту рівна Е_F, то для енергії F кристалу, який містить n дефектів, отримаємо

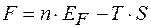(1.4)

Мінімізація вільної енергії F відносно числа n дефектів у виразі (1.4) приводить до наступного рівняння:

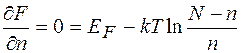(1.5)

Таким чином, отримаємо дуже важливе рівняння для визначення концентрації точкових дефектів при зміні темаператури, тобто

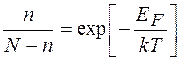. (1.6)

Якщо 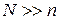, то атомна доля ізольованих дефектів визначається так:

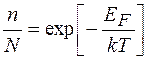. (1.7)

Як слідує із рівняння (1.7) концентрація точкових дефектів при Т=0 ⁰К швидко наростає із підвищенням Т.

Енергія Е_F (див.рис.1.8) визначається різницею енергій E_F=U(Q₁) - U(Q₀), в основному і дефектному станах. Значення Е_F для різних напівпровідників складає порядка 1–3 еВ.

При кімнатній температурі концентрація термофлуктуаційних дефектів нехтовно мала: Наприклад для Е_F = 2 еВ, Т = 300 ⁰К, 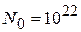см^-3 концентрація вакансій 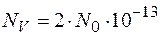см^-3, N₀ - число Авогадро

Вказане значення N_V знаходиться далеко за межами виявлення існуючими методами. Концентрація даних дефектів стає значною при температурах поблизу точки плавлення кристала Т_пл. Проте при таких температурах, як правило, утруднені експериментальні дослідження. Тому для вивчення термофлуктуаційних дефектів, зазвичай, використовують метод гартування: витримують зразок при Т >> Т_пл і потім різко охолоджують. При цьому значна частина утворених при високій температурі дефектів виявляється замороженою, тобто зберігається достатньо довго. У звичайних умовах вдається реалізувати швидкості охолоджування зразка DT/Dt ~ 10⁴ К/с. При використанні для нагріву поверхні кристала короткого (10^-11–10^-8 с) лазерного імпульсу величини DT/Dt складають 10⁹–10¹⁰ К/с і більше.

Очевидно, що дефекти, сформовані при загартуванні є нерівноважними. Підвищуючи температуру кристала до деякого значення Т і поволі потім охолоджуючи його, можна усунути гартівні дефекти. Така операція незалежно від причини виникнення дефектів називається відпалом. Переважна більшість дефектів відпалюються в Ge і Si при температурах 600 і 900 ⁰К відповідно протягом 30–60 хвилин.

Аналогічний термодинамічний розрахунок може бути проведений і для простих комплексів точкових дефектів. Наприклад, для дивакансій. Якщо координаційне число дорівнює z, то матимемо 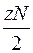сусідніх пар вузлів гратки в кристалі. Тоді дивакансії можуть бути розподілені наступним чином

. (1.8)

По аналогії із (1.7) одержимо:

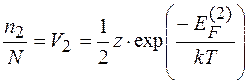, (1.9)

де 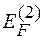- енергія утворення дивакансій.

Якщо 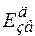енергія зв’язку вакансій у дивакансії, та 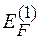енергія утворення однієї вакансії, то:

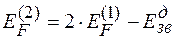. (1.10)

Тоді (1.9) можна переписати у вигляді:

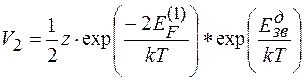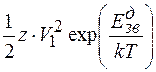=. (1.11)

Для випадку ГЦК гратки z =12, тоді співвідношення між концентраціями моновакансій (V₁₎ та дивакансій (V₂) запишеться у вигляді:

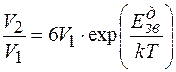(1.12)

Тут у співвідношенні (1.12) число 6 представляє число незалежних орієнтацій комплексу в гратці. Такого роду судження можна використати і для більш складних комплексів із вакансій чи міжвузольних атомів.

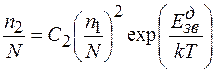
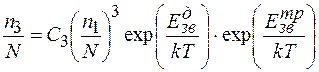, (1.13)

де 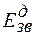та 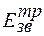- додаткові енергії зв’язку диванкансій та тривавансій.

Комбінаторні множники С₂ та С₃ можна знайти шляхом підрахунку числа незалежних орієнтацій комплексу. Простіше всього це зробити, визначивши спочатку число можливих орієнтацій, рахуючи дефекти різними, а потім врахувати нерозпізнаність дефектів, розділити одержаний результат на число можливих перестановок. Так для дивакансій в ГЦК гратці матимемо

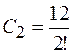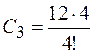=6 ; =2.

Контрольні питання

1. Від яких складових внутрішньої енергії залежить утворення точкових дефектів?

2. Дати пояснення визначенням «конфігураційна» та «коливна» ентропії.

3. Записати співвідношення, яке описує залежність концентрації вакансій від температури.

4. Записати співвідношення для визначення концентрації точкових дефектів втілення в ГЦК кристалах.

5. Оцінити енергію зв’язку дивакансій.

6. Чому утворення комплексів із дефектів є більш вигідним, ніж існування окремих точкових дефектів?

Розділ 2. Загальна теорія розупорядкування в твердих тілах.