Дисперсійні співвідношення для функцій Гріна.

Дисперсійні співвідношення - інтегральні рівняння, що зв'язують дійсну і уявну частини перетворення Фур'є функції відгукулінійної фізичної системи на зовнішні впливи. Є прямими наслідками фізичного принципу причинності і не залежать від конкретного механізму взаємодії системи із зовнішнім впливом.

Визначення

Нехай f (z) є комплексною функцією, аналітичність у верхній півплощині, та 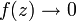при При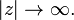пустимо, що має фізичний сенс функція F (x) є f (z) на речовій осі або, у разі наявності точки розгалуження, межа f (z) при z , Що прагне до речовій осі зверху.

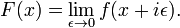
Дисперсійні співвідношення записуються у вигляді інтегральних рівнянь:

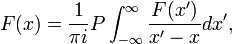
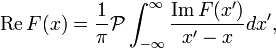
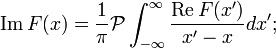
тут 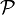- Символ інтеграла в сенсі головного значення. Дисперсійні співвідношення виводяться із застосуванням інтегральної формули Коші і, таким чином, не залежать від конкретної розглянутої моделі фізичного явища.

Фізичний зміст

"Відгук" 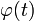лінійної системи на "обурення" 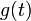можна записати у вигляді: 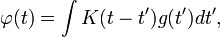де K (t) - функція Грінасистеми. Розглянуті функції f (z) являють собою перетворення Фур'є таких функцій Гріна: 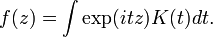Вимога причинності, що складається в неможливості виникнення відгуку раніше причини, означає, що K (t) = 0 при t <0 . Наслідком принципу причинності є те, що функція f (z) аналітична у верхній півплощині та 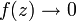при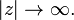

Застосовуються

В квантової теорії поля, при розрахунку амплітуд розсіювання. Дисперсійні співвідношення пов'язують безпосередньо одержувані з досвіду величини, такі як амплітуди ймовірностей або перетину різних переходів.

Вперше були отримані Крамерса і Кроніга в класичній теорії дисперсії, при вивченні залежності показника заломленнясередовища від частоти світла, для дійсної та уявної частини показника заломлення середовища