Поняття ентропії. Квантування фазового простору. Фізичний зміст ентропії.

.Ентропія — фізична величина, яка в спостережуваних явищах і процесах характеризує знецінювання (розсіювання) енергії, зумовлене перетворенням усіх її видів на теплову і рівномірним розподілом тепла між тілами (вирівнювання їхніх температур)

Ентропія – це функція стану, яка характеризується тим, що різниця ентропій у двох різних точках дорівнює сумі зведених теплот, які треба витратити на перехід з початкового стану 1 у кінцевий стан 2 по оборотному шляху.

Ентропія визначається з точністю до константи. Власне, фізичний зміст має не сама ентропія, а її різниця. Отже, за означенням

.

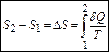це ми навели найзагальніший вираз для ентропії. Давайте обчислимо ентропію ідеального газу.

Із першого начала термодинаміки випливає, що

.

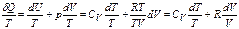Тоді

.

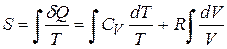Якщо 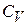не залежить від температури, то для ідеального газу у кількості 1 моль

,

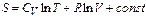звідки

.

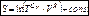Розглянемо адіабатний процес. 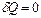, звідки 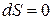. Отже, 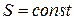, тому

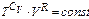, або , .

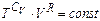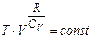Якщо скористатись рівнянням Роберта Майєра 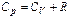, або 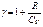, , 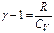маємо

,

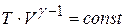тобто із виразу для ентропії ідеального газу отримали рівняння адіабати. Отже, адіабатний процес – ізоентропійний.

Ми звикли представляти всі діаграми у координатах 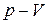. Простий аналіз циклу Карно показує, що його форма залежить від робочого тіла. Цикл Карно задається крім двох ізотерм двома адіабатами. Хід адіабати 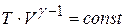залежить від коефіцієнта 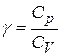, тобто від величини, яка визначається молекулярною будовою робочого тіла. Для одноатомного газу, нагадаю, 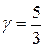, для двоатомного – 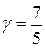, для трьохатомного – .

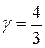Цікавим було б побудувати цикл, форма якого не залежала б від природи робочого тіла. Такий цикл можна побудувати у координатах 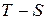(температура-ентропія), ця залежність називається ентропійною діаграмою.

Ізотерми у такому циклі перетворяться на горизонтальні прямі. А що можна сказати про адіабати ? Ми ж недаремно тільки що показали, що адіабатний процес ізоентропійний. Отже, адіабати можна представити як вертикальні прямі. Утворений цикл еквівалентний звичному циклу Карно у координатах 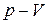, і ми це зараз доведемо.

Для цього визначимо к.к.д. утвореного циклу. Кількість теплоти, що передається нагрівачем робочому тілу на першій ізотермі

.

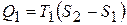Це випливає із означення ентропії. На адіабаті теплообміну немає. Ця кількість теплоти чисельно дорівнює площі прямокутника 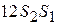. Аналогічно, кількість теплоти, яку передає холодильнику робоче тіло

.

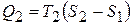Ця кількість теплоти чисельно дорівнює площі прямокутника 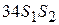. Тоді к.к.д.

.

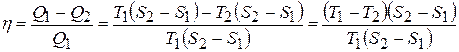Остаточно отримаємо

.

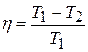Цей вираз співпадає із отриманим у доведенні першої теореми Карно, отже цикли еквівалентні. К.к.д. геометрично є відношенням заштрихованої площі циклу до площі прямокутника .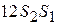

Давайте знову повернемось до необоротного процесу. А також до звичних координат 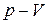. Нехай у результаті необоротного процесу система перейшла із початкового стану 1 у рівноважний стан 2. Чи можна зобразити графічно необоротний процес ? Ні, зобразити можна лише процес, який відтворюється. А необоротний процес щоразу щось змінює у оточуючому середовищі. Тому необоротний процес зобразити неможливо. Ми його проведемо умовно штриховою лінією. Після закінчення необоротного процесу ми повернемо систему у вихідний стан за допомогою оборотного процесу. Він зображений суцільною лінією. Отриманий процес є необоротним, оскільки необоротною є його частина (спросить !).

Запишемо нерівність Клаузіуса для такого необоротного колового процесу :

.

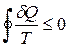Розіб’ємо коловий інтеграл на два :

.

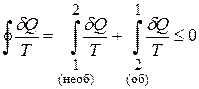Другий доданок виражає зміну ентропії системи при оборотному процесі, тобто

.

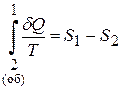Тоді нерівність Клаузіуса набуває вигляду

,

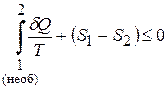або

.

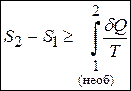Отримана нерівність є нарешті кількісним формулюванням другого начала термодинаміки. Хоча треба зазначити, що і з цим формулюванням не все гаразд. Обмеження виникає через наявність інтегралу, оскільки ми прив’язуємось до форми шляху. Остаточно, найбільш загальним є кількісне формулювання другого начала термодинаміки у диференціальній формі (оскільки ентропія є функцією стану за означенням, то беремо її повний диференціал) :

.

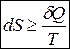Зміна ентропії завжди не менша за кількість зведеної теплоти. Знак рівності відноситься до оборотних процесів, а знак нерівності до необоротних процесів. А для циклічного (колового) процесу

,

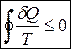що має прозорий зміст, оскільки ентропія є функцією стану, то коли ми повертаємось у вихідний стан, то й ентропія повертається до вихідного значення.

Об’єднавши вирази для першого і другого начал термодинаміки можемо записати нерівність

.

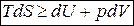Цей вираз є математичним записом основного рівняння термодинаміки, яке об’єднує перше і друге начала термодинаміки.

Ентропія

Звичайно всякий процес, при якому система переходить із одного стану в інше, протікає таким чином, що не можна провести цей процес у зворотному напрямку так, щоб система проходила через ті ж проміжні стани, і при цьому в навколишніх тілах не відбулися які-небудь зміни. Це пов'язане з тим, що в процесі частина енергії розсіюється, наприклад, за рахунок тертя, випромінювання й т.п. Т. ч. практично всі процеси в природі необоротні. У будь-якому процесі частина енергії губиться. Для характеристики розсіювання енергії вводиться поняття ентропії. (Величина ентропії характеризує тепловий стан системи й визначає ймовірність здійснення даного стану тіла. Чим більш імовірно дане стану, тим більше ентропія.) Усі природні процеси супроводжуються ростом ентропії. Ентропія залишається постійної тільки у випадку ідеалізованого оборотного процесу, що відбувається в замкненій системі, тобто в системі, у якій не відбувається обмін енергією із зовнішніми стосовно цієї системи тілами.

Ентропія і її термодинамічний зміст:

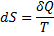
Энтропия – это такая функция состояния системы, бесконечно малое изменение которой в обратимом процессе равно отношению бесконечно малого количества теплоты, введенного в этом процессе, к температуре, при которой оно вводилось.

У кінцевому оборотному процесі зміни ентропії може бути підраховане по формулі:

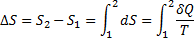
де інтеграл береться від початкового стану 1 системи до кінцевого стану 2.

Оскільки ентропія є функція стану, то властивістю інтеграла 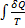є його незалежність від форми контуру (шляху), по якому він обчислюється, отже, інтеграл визначається тільки початковим і кінцевим станам системи.

У будь-якому оборотному процесі зміна ентропії рівно 0

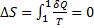(1)

У термодинаміці доводиться, що S системи здійснюючої необоротний цикл зростає

Вираження (1) і (2) відносяться тільки до замкнених систем, якщо ж система обмінюється теплотою із зовнішнім середовищем, то її S може поводитися будь-яким чином.

Співвідношення (1) і (2) можна представити у вигляді нерівності Клаузиуса

ΔS ≥ 0

т.т. ентропія замкненої системи може або зростати (у випадку необоротних процесів) або залишатися постійної (у випадку оборотних процесів).

Якщо система робить рівноважний перехід зі стану 1 у стан 2, то зміни ентропії

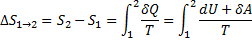
де dU і δA записується для конкретного процесу. По цій формулі ΔS визначається з точністю до адитивної постійної. Фізичний зміст має не сама ентропія, а різниця ентропії. Знайдемо зміну ентропії в процесах ідеального газу.

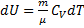
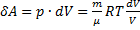
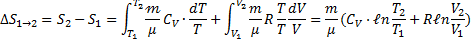
т.т. зміна ентропії S ΔS1→2 ідеального газу при переході його зі стану 1 у стан 2 не залежить від виду процесу.

Т.як для адіабатичного процесу δQ= 0, то ΔS = 0 => S = const, тобто адіабатичний оборотний процес протікає при постійній ентропії. Тому його називають ізоентропійним.

При ізотермічному процесі (T = const; T1 = T2: )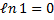

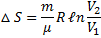
При ізохорному процесі (V = const; V1 =V2; )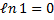

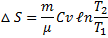
Ентропія має властивість адитивності: ентропія системи дорівнює сумі ентропії тіл вхідних у систему. S = S1 + S2 + S3 + ... Якісною відмінністю теплового руху молекул від інших форм руху є його хаотичність, безладність. Тому для характеристики теплового руху необхідно ввести кількісну міру ступеня молекулярного безладдя. Якщо розглянути який-небудь даний макроскопічний стан тіла з певними середніми значеннями параметрів, то воно є щось інше, як безперервна зміна близьких мікростанів, що відрізняються друг від друга розподілом молекул у різних частинах об'єму, що й розподіляється енергією між молекулами. Число цих безперервних, що поміняють один одного мікростанів, характеризує ступінь безладності макроскопічного стану всієї системи, w називається термодинамічною ймовірністю даного мікростану. Термодинамічна ймовірність w стану системи — це число способів, якими може бути реалізоване даний стан макроскопічної системи, або число мікростанів, що здійснюють даний мікростан (w ≥ 1, а математична ймовірність ≤ 1).

За міру несподіванки події вмовилися приймати логарифм його ймовірності, узятий зі знаком мінус: несподіванка стану рівна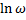

Згідно Больцману, ентропія S системи й термодинамічна ймовірність зв'язані між собою в такий спосіб:

S=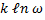

де 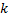-постійна Больцмана ( 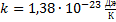). Таким чином, ентропія визначається логарифмом числа станів, за допомогою яких може бути реалізований даний мікростан. Ентропія може розглядатися як міра імовірності стану т/д системи. Формула Больцмана дозволяє дати ентропії наступне статистичне тлумачення. Ентропія є мірою невпорядкованості системи. Насправді, чим більше число мікростанів, що реалізують даний мікростан, тим більше ентропія. У стані рівноваги системи - найбільш імовірного стану системи – число мікростанів максимально, при цьому максимальна й ентропія.

Т.як реальні процеси необоротні, то можна затверджувати, що всі процеси в замкненій системі ведуть до збільшення її ентропії - принцип зростання ентропії. При статистичному тлумаченні ентропії це означає, що процеси в замкненій системі йдуть у напрямку збільшення числа мікростанів, іншими словами, від менш імовірних станів до більш імовірних, доти, поки ймовірність стану не стане максимальною.