Поняття про S-матрицю. Теорема Віка. Рівняння Дайсона.
Матриця розсіяння або S-матриця - оператор, який зв'язує між собою початкову і кінцеву хвильові функції квантової системи при розсіянні. Позначається зазвичай 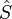 :
:
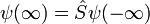 .
.
де  позначає хвильову функцію в нескінченно віддалений момент часу в минулому, до акту розсіяння, коли частинки перебувають дуже далеко одна від одної і взаємодією між ними можна знехтувати, а
позначає хвильову функцію в нескінченно віддалений момент часу в минулому, до акту розсіяння, коли частинки перебувають дуже далеко одна від одної і взаємодією між ними можна знехтувати, а 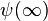 позначає хвильову функцію в нескінченно віддалений момент часу після акту розсіяння, коли знову ж, частинки вже встигли розлетітися на таку віддаль, що взаємодією між ними можна знехтувати.
позначає хвильову функцію в нескінченно віддалений момент часу після акту розсіяння, коли знову ж, частинки вже встигли розлетітися на таку віддаль, що взаємодією між ними можна знехтувати.
S-матриця унітарна, тобто
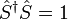 ,
,
де значок 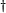 позначає ермітове спряження.
позначає ермітове спряження.
Оператор

називають оператором переходу.
Гамільтоніан системи частинок, які розсіюються одна на іншій можна записати у вигляді
 .
.
В цьому виразі гамільтоніан ситеми частинок до розсіяння і після нього розбивається на різні складові для загальності — при зіткненнях склад системи може змінитися, наприклад, електрон може вибити інший електрон із атома.
Якщо функції 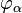 є власними функціями оператора
є власними функціями оператора  :
:
 ,
,
а функції 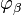 є власними функціями оператора
є власними функціями оператора 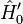 :
:
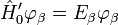 ,
,
то хвильову функцію початкового і кінцевого станів можна розкласти
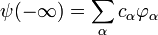
 Тоді
Тоді 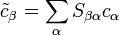
Із цього виразу видно, що  є матрицею, загалом нескінченного рангу. Завдяки цьому S-матриця й отримала свою назву.
є матрицею, загалом нескінченного рангу. Завдяки цьому S-матриця й отримала свою назву.
Імовірність переходу системи із стану 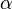 в стан
в стан  визначається елементом матриці переходу
визначається елементом матриці переходу 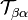 :
:
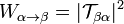
Беручи до уваги, що енергія системи є інтегралом руху, матрицю переходу запишемо у вигляді:

Тоді загальна імовірність переходу за нескінченний проміжок часу  дорівнює:
дорівнює:

Імовірність переходу в одиницю часу  одержимо, поділивши повну імовірність
одержимо, поділивши повну імовірність  на повний проміжок часу
на повний проміжок часу  :
:
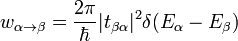
Ряд Дайсона — ряд збурень у теорії розсіяння, кожен із членів якого можна зобразити у вигляді діаграми Фейнмана. Ряд носить ім'я Фрімена Дайсона і є загалом розбіжним, однак, уже другий член цього ряду в квантовій електродинаміці дозволяє отримати точність до 10−10 завдяки малості сталої тонкої структури.
Побудова ряду Дайсона використовує поняття часового упорядкування.
Вивчається система, що описується гамільтоніаном, який є сумою незбуреної частини й збурення:
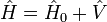
У зображенні взаємодії оператор еволюції хвильової функції  задовольняє рівнянню Томонаги-Швінгера
задовольняє рівнянню Томонаги-Швінгера
 , де
, де 
або інтегродиференціальному рівнянню
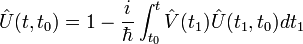
Підставляючи оператор еволюції з лівої частини в праву можна отримати нескінченний ряд:

Дайсон запропонував розширити інтегрування в кожному інтегралі від 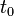 до
до 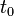 , але вимагати, щоб оператори завжди були упорядковані в часі, тобто в добутку
, але вимагати, щоб оператори завжди були упорядковані в часі, тобто в добутку 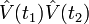 , наприклад, завжди було
, наприклад, завжди було 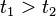 . Тоді кожен із доданків ряду збільшиться в
. Тоді кожен із доданків ряду збільшиться в 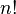 разів.
разів.
Як наслідок n-ний член ряду матиме вигляд:
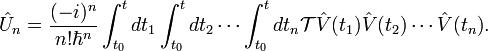 , де
, де 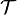 - оператор часового упорядкування.
- оператор часового упорядкування.
Як наслідок, ряд Дайсона можна записати в компактному вигляді:
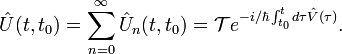
Формула Вика — формула теории вероятностей, выражающая математическое ожидание многочлена от координат гауссовского вектора через элементы матрицы ковариаций. Одним из её применений является связь между средним значением полинома от следов степеней случайной матрицы большого размера и родамиповерхностей, получаемыми склейкой заданных многоугольников при различных отождествлениях сторон
Теорема.
Пусть  — гауссов вектор с нулевым математическим ожиданием,
— гауссов вектор с нулевым математическим ожиданием, 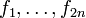 — линейные функции от
— линейные функции от 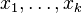 . Тогда
. Тогда

где суммирование в правой части ведётся по всем разбиениям множества 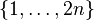 на пары
на пары 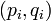 с
с

(тем самым, каждое разбиение оказывается посчитано ровно один раз)
В качестве пояснения формулировки теоремы приведём несколько примеров:
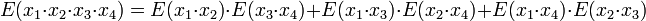
Дата добавления: 2015-06-01; просмотров: 1139;
