Елементи оптимізаційних розрахунків ССТ: відносні розміри, екстремуми функцій мети, обмеження, принципи компромісної багатофакторної оптимізації

Система відносних одиниць (англ. per-unit system) — спосіб розрахунку параметрів в системах передачі електроенергії, при якому значення системних величин (напруг, струмів, опорів, потужностей і тому подібне) виражаються як множники певної базової величини, прийнятої за одиницю. Це спрощує обчислення, оскільки величини, виражені в відносних одиницях, не залежать від рівня напруги. Так, для пристроїв (наприклад, трансформаторів) одного типа, падіння напруги і втрати потужності при різних рівнях напруги розрізнятимуться по абсолютній величині, але виражені відносно базових величин, будуть приблизно однакові. Після розрахунку отримані результати можуть бути переведені назад в системні одиниці (вольти, ампери, оми, вати і тому подібне), якщо відомі базові величини, прийняті за основу. Відносні одиниці використовуються зазвичай при розрахунках передавальної потужності; проте, оскільки параметри устаткування (трансформаторів, моторів і генераторів) часто вказуються у відносних величинах, кожен електромеханік має бути знайомий з їх концепцією. У системі відносних одиниць використовуються одиниці потужності, напруги, сили струму і т.д. Лише дві з них є незалежними; зазвичай як незалежні величини вибираються потужність і напруга, що продиктоване природою реальних енергосистем. Всі системні величини в мережі виражаються як множники вибраних базових значень. Наприклад, для потужності як база може бути вибрана номінальна потужність трансформатора (або інколи довільна потужність, така, що набутих відносних значень полегшують обчислення). Як база для напруги зазвичай вибирається номінальна напруга шини. У технічній літературі англійською мовою різні типи величин позначаються одним і тим же символом pu (інколи p.u.). З контексту має бути зрозуміле, чи йде мова про напругу, силі струму і так далі

Екстремуми функцій мети.

Для визначення локальних екстремумів використовується наближений метод послідовно - одиночного покриття . Суть методу полягає в наступному. Мінімізація функції мети здійснюється по групах перемінних. У групу вибираються параметри розміщення одного покриваючого кола. Це дозволяє звести задачу мінімізації функції, яка задана в просторі 2п, до п- кратної оптимізації в 2-х вимірних просторах. Щоразу після розв'язку чергового етапу задачі оптимізації визначаються і фіксуються параметри розміщення покриваючого кола. Алгоритм реалізації методу послідовно-одиночного покриття можна записати у виді наступної ітераційної формули:

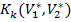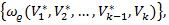=max (10)

де (10) - функція кіл 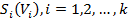і області :

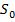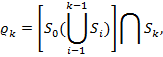
k=1,2,…,n.

На рис. 3.1 приведені послідовно одержувані часткові покриття області S0 при розміщенні кіл S1…S2 .

У випадку, коли найбільше значення функції 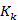досягається не в одній точці 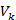, а на

множині точок, у якості 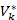вибираються координати точки, що належить непокритій

частині області для якої виконуються умови (4.4).

Метод послідовно-одиночного покриття дає можливість порівняно легко одержувати наближення до локальних екстремумів. Вибір місця розташування першого покриваючого об'єкта і порядок розміщення кіл однозначно визначають деяке наближення до локального екстремуму функції мети і відповідну точку в області припустимих розв'язків. Оскільки в роботі розглядаються кола рівного радіуса, то зміна порядку розміщення кіл не приводить до нового наближення до оптимуму. У зв'язку з цим, лише нове місце розташування першого покриваючого кола приводить до нового наближення до локального екстремуму.

Таким чином, можна установити відповідність між вибором місця розташування першого покриваючого кола і наближеннями до локальних екстремумів функції мети. Цей факт дає можливість розбити процес розв'язку задачі покриття на два етапи: визначення наближень до локальних екстремумів функції мети й організацію перебору одержуваних наближень. На першому етапі застосовується метод послідовно-одиночного покриття, на другому - методи їхнього перебору (повного - у випадку невеликої кількості покриваючих кіл і усіченого, що використовує особливості функціоналів, що оптимізуються, на комбінаторних множинах).

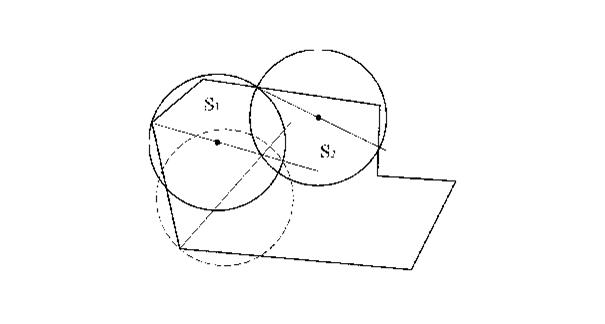
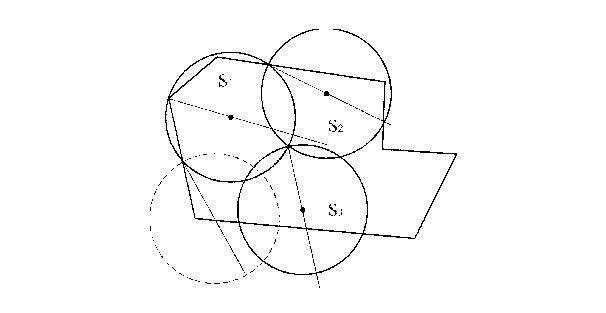
Рис. 3.1 Послідовні часткові покриття кругами , довільної області

1. Функція мети

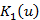, у загальному випадку кусочно-пладка, причому нелінійна на кожній гладкій ділянці. Простір параметрів, у якому визначена функція мети, залежить від числа об'єктів п і має розмірність 2n

2. Область припустимих розв'язків 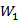задається у виді однієї нерівності (3.7). Ця нерівність зв'язує всі параметри покриття кіл, що належать до неопуклої, багато зв'язної області припустимих розв'язків.

3. У силу нелінійності функції мети і неопуклості області її визначення, задача покриття, що розглянута в роботі, є багатоекстремальною. Екстремуми функції мети можуть знаходитися як усередині області припустимих розв'язків, так і на її границі.

Багатокритеріальна оптимізація за результатами досліджень. Розв'язанням задач оптимізації складних технологічних і технічних систем притаманна істотна специфіка, зумовлена прикладною спрямовані­стю одержаних розв'язків; відсутністю інформації про механізми явищ або процесів, що відбуваються в систе­мі; значною кількістю показників якості (критеріїв оптимальності) і факторів, які беруть участь в оптимізації та моделюванні; випадковим характером зміни критеріїв оптимальності та деяких факторів. Раніше були вибрані

критерії якості у і, у 2 •

Якщо задають кількість критеріїв оптимізації більше ніж один, то їх спільні значення вибирають, вико­ристовуючи принцип компромісу за Парето :

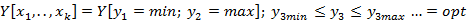(11)

де У- узагальнений критерій оптимальності об'єкта оптимізації, одержаний шляхом використання принципу компромісу за Парето.

Ідея компромісу за Парето полягає в пошуку таких умов функціонування системи, за якими узагальне­ний критерій оптимальності її досягає екстремального значення. Узагальнений критерій оптимальності

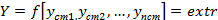, (12)

де У2ст,..,Упст ~ стандартизовані значення критеріїв якості. Останні можна визначити за формулою:

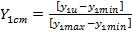(13)

де y_lM - значення функції відгуку при и-м поєднанні умов функціонування системи; >'_lmin - мінімальне з усіх результатів значення 1-ої функції відгуку; у_ІШХ - максимальне з усіх результатів значення І-оі функції відгуку.

Легко довести, що 0 < у_Хст < 1. Отже, будь-яку функцію відгуку зводять до сегмента [0,1] і виража­ють стандартизованим значенням у_1ст у просторі функцій відгуків.

Цей простір являє собою куб розмірності п, ребра якого складають стандартизовані значення крите­ріїв якості як система ортогональних координат. Кожне ребро куба є одним із значень 0 < у_1ст < 1. За опти­мальне значення Y = opt беруть таку точку 1 < і/ < N з простору функцій відгуків, яка буде найближчою до ідеальної комбінації значень цих відгуків.

Враховуючи, що в загальному випадку до відгуків ставлять вимоги екстремальності, тобто відповід­ність відгуку максимуму або мінімуму, ідеальному поєднанню вимог буде відповідати одна з вершин куба, що розглядають, для якої ці вимоги виконуються. Компроміс за Парето виконуватиметься для такої точки, відстань від якої до зазначеної вершини буде мінімально.