Amp; 5.2. Неперервність функцій.
При побудові графіків найпростіших функцій ми використовували властивості неперервних функцій, хоча сам термін «неперервна функція» не вживався, а саме : на площині відмічалися точки, координати яких занесені в таблицю, сполучивши відмічені точки суцільною лінією, одержували графік функції. Це можна зробити не завжди, а тільки в тому випадку, якщо функція неперервна.
Означення. Функція 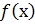 називається неперервною в точці
називається неперервною в точці 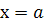 , якщо границя функції при
, якщо границя функції при 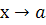 існує і дорівнює значенню функції при
існує і дорівнює значенню функції при 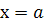 :
:
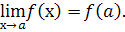
Із означення неперервності функції 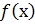 в точці
в точці 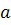 , випливає виконання слідуючих умов :
, випливає виконання слідуючих умов :
1) функція 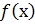 повинна бути визначена в точці
повинна бути визначена в точці 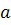 ;
;
2) у функції 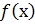 повинна існувати границя в точці
повинна існувати границя в точці 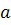 ;
;
3) границя функції в точці 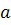 співпадає із значенням функції в цій точці.
співпадає із значенням функції в цій точці.
Приклад 1. Дослідити на неперервність функцію 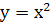 в точці
в точці 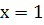 . Функція
. Функція 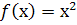 визначена на всій числовій прямій і
визначена на всій числовій прямій і
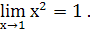
Так як 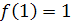 , тобто значення функції в точці
, тобто значення функції в точці 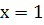 співпадає з границею при
співпадає з границею при 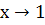 , то згідно означення, функція
, то згідно означення, функція 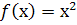 неперервна в точці
неперервна в точці 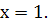
Функція називається неперервною зліва в точці 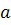 , якщо
, якщо
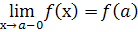
і неперервною справа в точці 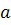 , якщо
, якщо
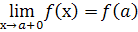
Приклад 2. Дослідити неперервність в точці 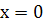 функцію
функцію 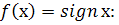
| у |
| х |
| -1 |
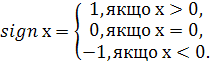
Функція при 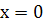 визначена і дорівнює 0.
визначена і дорівнює 0.
Із малюнка видно, що
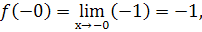
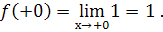
Отже, 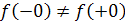 , тобто границі існують, але різні, тому функція не є неперервною в точці
, тобто границі існують, але різні, тому функція не є неперервною в точці 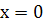 .
.
Приклад 3. Функція 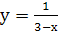 не є неперервною в точці
не є неперервною в точці 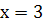 , так як вона не визначена в цій точці.
, так як вона не визначена в цій точці.
Функція називається неперервною в проміжку, якщо вона неперервна в усіх точках цього проміжку.
Дата добавления: 2015-06-27; просмотров: 1397;
