Теорія атома гелію.

Атом гелия (He), второй атом периодической системы, является наиболее простым из многоэлектронных атомов. Однако уже на нем, в отличие от водорода, классическая механика потерпела полный крах.

Попытки рассчитать его энергию классическими методами (с учетом квантовых постулатов Бора) привели к выводу о невозможности применения классической механики к атомным системам с двумя и б´ольшим числом электронов. Современная же квантовая теория не встречает принципиальных трудностей в исследовании таких объектов. Вычислительные трудности весьма значительны, что не позволяет получить наблюдаемые характеристики атома гелия в замкнутой аналитической форме, не говоря уже о более сложных атомах. Поэтому в настоящей лекции будут развиты некоторые приближенные методы исследования реальных двухэлектронных систем и с их помощью получена структура энергетического спектра не только в атоме гелия (с зарядовым числом ядра Z = 2), но и в двухэлектронных гелиеподобных ионах:

Li+ (Z = 3), Be2+ (Z = 4) и др.

Атом и атомные системы могут длительно пребывать только в особенных стационарных или квантовых состояниях, каждому из которых отвечает определенная энергия. В стационарном состоянии атом не излучает электромагнитных волн.

Излучение света происходит при переходе электрона из стационарного состояния с большей энергией в стационарное состояние с меньшей энергией. Энергия излученного фотона равна разности энергий стационарных состояний.

Для получения энергетических уровней в атоме водорода в рамках модели Бора записывается второй закон Ньютона для движения электрона по круговой орбите в поле кулоновской силы тот притяжения

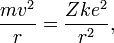где m — масса электрона, e — его заряд, Z — количество протонов в ядре (атомный номер) и k — кулоновская константа, зависящая от выбора системы единиц. Это соотношение позволяет выразить скорость электрона через радиус его орбиты:

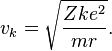
Энергия электрона равна разности кинетической энергии движения и его потенциальной энергии:

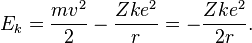
Используя правило квантования Бора, можно записать:

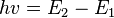
откуда радиус орбиты выражается через квантовое число n. Подстановка радиуса в выражение для энергии даёт:

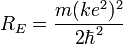≈ 13,6 эВ

называется постоянной Ридберга. Она равна энергии связи электрона в атоме водорода в основном состоянии, т.е. минимальной энергии, необходимой для ионизации атома водорода в низшем (стабильном) энергетическом состоянии.