Волновые функции атома водорода

Векторы состояния атома водорода удобно представлять в пространственном базисе:

| F ñ = C₁| 1 ñ + C₂| 2 ñ + • • • = SC_i| i ñ ,

где каждое базисное состояние | i ñ отличается тем, что для него точно известны положения обеих частиц в пространстве относительно фиксированной лабораторной системы координат, т.е. известны 6 чисел-координат (x₁, y₁, z₁, x₂, y₂, z₂)_i. Ясно, что с таким бесконечномерным вектором состояния можно практически работать только после его перевода в функциональное представление — волновую функцию. Эти волновые функции, описывающие любые состояния атома, допустимые законами квантовой механики, должны, в общем случае, зависеть от шести пространственных координат и от времени: Ф = Ф(x₁, y₁, z₁, x₂, y₂, z₂; t). В дальнейшем ограничимся рассмотрением только стационарных состояний (нестационарные состояния не представляют интереса для химической проблематики, поскольку время их жизни, как правило, не превышает 10^–8 с), для которых волновую функцию можно представить в виде произведения пространственного и временного множителей:

Ф(x₁, y₁, z₁, x₂, y₂, z₂; t) = Ф(x₁, y₁, z₁, x₂, y₂, z₂) × exp(iwt), где w = Е/h

В результате задача сводится к установлению вида пространственного множителя Ф(x₁, y₁, z₁, x₂, y₂, z₂) и значения энергии Е, которые можно найти из уравнения на собственные значения: НФ = ЕФ.Оператор Гамильтона для данной системы включает в себя три слагаемых: два одночастичных оператора кинетической энергии (Т₁ и Т₂) и двухчастичный оператор потенциальной энергии (U₁₂):

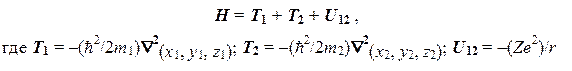
Здесь символ Ѳ (иногда вместо него употребляется эквивалентный символ D) обозначает одночастичный оператор "набла-квадрат", представляющий собой сумму вторых частных производных по декартовым координатам некоторой частицы:

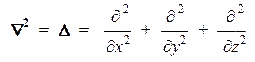
Таким образом, интересующее нас уравнение на собственные значения (т.н. "стационарное уравнение Шредингера") имеет вид:

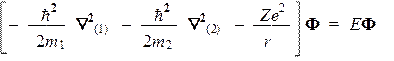
Решениями этого уравнения являются волновые функции, описывающие все возможные стационарные состояния атома водорода, а также соответствующие им энергии (в нерелятивистском приближении, т.е. без учета магнитных эффектов). Если атом изолирован от окружающих тел, то движения частиц в нем можно разделить на два типа:

1) глобальное движение атома как материальной точки (центра масс) в лабораторной системе координат (X, Y, Z).

2) локальные движения частиц во внутренней системе координат (x, y, z), начало которой расположено в центре масс.

Первый тип движения можно исследовать, смотря на атом "издалека", т.е. полагая его просто материальной точкой без внутренней структуры. Второй тип движения можно исследовать, смотря на атом "изнутри" и полагая, что атом как целое является неподвижным. В этом случае наблюдатель находится в центре масс и видит лишь относительное движение электрона и ядра. Независимость внешнего и внутреннего движений позволяет представить шестимерную волновую функцию в виде произведения двух трехмерных функций:

Ф(x₁, y₁, z₁, x₂, y₂, z₂) = Ф' (X, Y, Z) × Ф''(x, y, z)

Первый сомножитель представляет собой глобальную функцию, описывающую движение атома как целого (т.е. как одной бесструктурной частицы с массой M = m₁ + m₂) и удовлетворяет трехмерному уравнению:

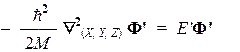
Это стандартное уравнение для свободной частицы с массой М. Его решения известны из модельных квантовомеханических задач "свободная частица" и "частица в трехмерном потенциальном ящике" (см. [3]).

Второй сомножитель представляет собой "внутреннюю" функцию, описывающую движение электрона и ядра относительно неподвижного центра масс. Согласованный характер движения электрона и ядра дает возможность заменить их единственной "квазичастицей", обладающей массой m и движущейся вокруг неподвижного центра масс. Вследствие большого различия в массах электрона и ядра эта квазичастица по своим свойствам практически совпадает с электроном. Поэтому в дальнейшем будем рассматривать ее как обычный электрон с незначительно уменьшенной массой. Внутренняя функция, описывающая движение электрона (квазичастицы), удовлетворяет трехмерному уравнению вида:

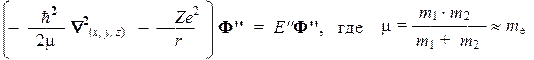
В декартовой системе координат это уравнение невозможно сделать более простым, так как входящая в него переменная r зависит от всех трех декартовых координат электрона: r² = x² + y² + z². Поэтому целесообразно перейти к сферической системекоординат, в которой переменная r является независимой координатой. Замена производится по правилам:

x = r × sinq × cosj ; y = r × sinq × sinj ; z = r × cosq

где угол q отсчитывается в вертикальной плоскости от оси z и изменяется в интервале от 0 до p, а угол j отсчитывается в горизонтальной плоскости от оси x и изменяется в интервале от 0 до 2p. После замены переменных волновая функция изменяет свой вид: Ф''(x, y, z) ¾® Y(r, q, j), а стационарное уравнение Шредингера приобретает такую форму:

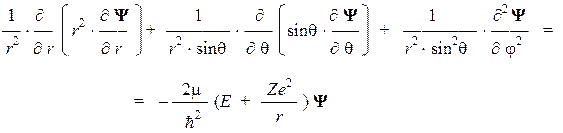
Сделанная замена переменных позволяет представить трехмерную функцию в виде произведения трех одномерных функций-сомножителей:

Y(r, q, j) = R(r) × Q(q) × F(j)

которые являются решениями системы из трех одномерных уравнений:

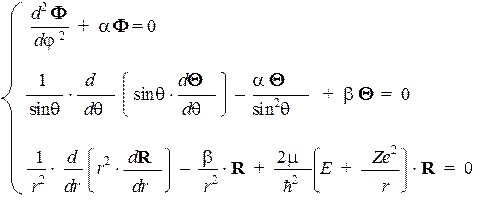
Необходимо отметить, что в результате процедуры разделения в уравнениях появились две новые константы — a и b, которые учитывают существующие взаимосвязи между уравнениями и их решениями. Эти параметры должны иметь одни и те же значения во всех уравнениях, куда они входят. Данное условие выполняется только для некоторых "разрешенных" значений, образующих дискретный набор, а именно:

a = 0, 1, 4, 9, 16, 25, … и b = 0, 2, 6, 12, 20, 30, 42, …

С целью упрощения этих рядов удобно ввести два новых вспомогательных параметра — l и m, для которых выполняются более простые условия:

b = l(l+ 1) , где l = 0, 1, 2, . . .

a = m × m , где m = 0, ±1, ±2, . . .

Дискретность в решениях R-, Q- и F-уравнений, вызываемая приведенными ограничениями для параметров a и b, приводит, в свою очередь, к дискретности допустимых значений энергии атома (она входит в R‑уравнение), связанной с внутренним движением:

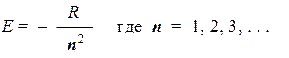
Целые числа, входящие в приведенные формулы, называются квантовыми числамиатома водорода: n — главное, l — орбитальное, m — магнитное. Они выступают в роли параметров, нумерующих возможные решения уравнения Шредингера, или, что то же самое, волновые функции стационарных состояний:

Y(r, q, j) = R(r) • Q(q) • F(j) = Y(n, l, m) =

= R(n, l) • Q(l, m) • F(m) = R(n, l) • Y(l, m)

Произведения Q(l, m) • F(m) = Y(l, m)называются шаровыми функциями.

Приведем явный вид Q-иF-функций (в сферических координатах):

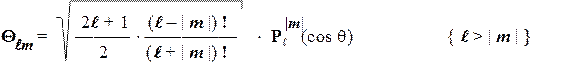
В этом уравнении символом Р обозначен т.н. "присоединенный полином Лежандра" степени l и порядка |m|, представляющий собой некоторую степенную функцию от (cos q). Явный вид этих полиномов можно найти в справочниках или вычислить по следующей формуле:

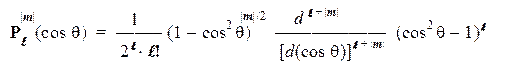
Для R-уравнения решения имеют вид:

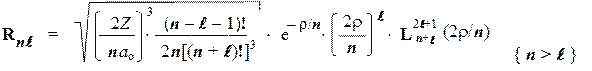
Здесь символом Lобозначен т.н. "присоединенный полином Лаггера" степени (n + l) и порядка (2l + 1) — степенная функция от новой переменной r = (Z/a_o)×r, которая представляет собой шкалу расстояний: прокалиброванную с помощью т.н. "атомных единиц длины" а_о = 4pe_oh²/me² » 0,053 нм (здесь константа e_o = 8,84×10^–12 ф/м — диэлектрическая постоянная).

Явный вид присоединенных полиномов Лаггера можно найти в справочниках или вычислить по формуле:

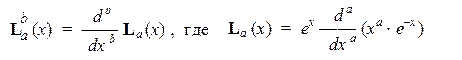
Стоящие впереди полиномов Лежандра и Лаггера сложные выражения являются нормировочными множителями, которые при задании конкретных величин квантовых чисел приобретают простой вид.

Следует обратить внимание на важное обстоятельство. В формулы входят некоторые величины, являющиеся факториалами типа х!. Эта функция определена только для целых неотрицательных чисел х. В результате, на допустимые совместные (т.е. относящиеся к одному состоянию атома) значения квантовых чисел накладываются ограничения, указанные выше в фигурных скобках.

Для иллюстрации можно привести конкретные выражения для волновых функций с небольшими номерами.

R-функции (нормировочные множители опущены):

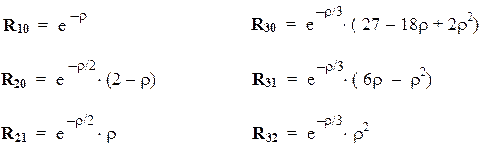
(В обозначениях функций первый числовой индекс равен главному квантовому числу n, а второй — орбитальному квантовому числу l.)

Q-функции(нормировочные множители опущены):

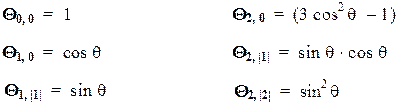
(В обозначениях функций первый числовой индекс равен орбитальному квантовому числу l, а второй — модулю магнитного числа |m|.)

Ф-функции(нормировочные множители опущены):

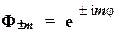
Располагая таблицами таких функций, можно легко построить явный вид волновой функции для любого стационарного состояния атома водорода. Пусть, например, состояние характеризуется набором квантовых чисел {n, l, m} = {2, 1, –1}. Тогда волновая функция будет иметь вид (нормировочный множитель опущен):

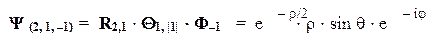
Полный вид волновой функции можно получить при умножении этой пространственной части на временной экспоненциальный множитель:

Y_{(2, 1, –1), t} = Y_{(2, 1, –1)} ×exp[i(E₂/h)t] ,

где Е₂ — энергия, соответствующая значению n = 2.

Обозначаемые тремя индексами функцииY_n,l,m часто называют водородными атомными орбиталями или Н-АО. Заметим, что в большинстве случаев они содержат комплексную экспоненту и, следовательно, являются комплекснозначными функциями. Это обстоятельство часто отмечается и в названии — комплексные атомные орбитали (КАО).

Существует еще одна, более удобная, номенклатура Н-АО. Каждый тип АО обозначается определенным символом — латинской буквой — указывающим на значение орбитального квантового числа:

Впереди буквы-символа указывается значение главного квантового числа, а магнитное квантовое число обозначается цифровым подстрочным индексом, следующим за буквой-символом. Например:

Y ₁₀₀ = 1s_o

Y ₂₀₀ = 2s_o Y ₂₁₀ = 2p_o Y _21–1 = 2p_–1 Y ₂₁₁ = 2p₁

Y ₃₀₀ = 3s_o Y ₃₁₀ = 3p_o Y _31–1 = 3p_–1 Y ₃₁₁ = 3p₁

Y ₃₂₀ = 3d_o Y ₃₂₁ = 3d₁ Y _32–1 = 3d_–1 . . . и т.д.

В ряде случаев бывает более удобным использование не самих волновых функций, а некоторых линейных комбинаций, построенных из этих функций, с целью получить чисто действительные функции. Такие линейные комбинации строятся в виде суммы или разности двух КАО, у которых все квантовые числа одинаковы по величине, но магнитные числа противоположны по знаку. У таких пар КАО R- и Q-сомножители в точности одинаковы, поскольку они не зависят от знака магнитного числа. В результате получаются суммы и разности комплексно сопряженных экспонент, которые сводятся к действительным тригонометрическим функциям (здесь нормировочные множители опущены):

Y_{(n, l, m)} + Y_{(n, l, –m)} = RQ(eimj +e–imj )= RQ• cos (mj) = Y⁺_{( n, l, |m|)}

Y_{(n, l, m)} – Y_{(n, l, –m)} = RQ(eimj – e–imj )= RQ• sin (mj) = Y ^–_{( n, l, |m|)}

Такие линейные комбинации называются действительными атомными орбиталями (ДАО). В их обозначениях нижний индекс заменяется на буквенный. Например, для АО p-типа имеем:

(2р₁ + 2р_–1) ~ 2p_x (2р₁ – 2р_–1) ~ 2p_y 2р₀ ~ 2p_z

или для АО d-типа:

(3d₁ + 3d_–1) ~ 3d_xz (3d₁ – 3d_–1) ~ 3d_yz

(3d₂ + 3d_–2) ~ 3d(x²– y²) (3d₂ – 3d_–2) ~ 3dxy 3d₀ ~ 3dz²

ДАО удобны в том отношении, что их можно изображать графически, анализировать различные пространственные характеристики и симметрию. Подчеркнем, что наборы КАО и ДАО полностью эквивалентны в математическом отношении и представляют собой два базисных набора в одном и том же пространстве состояний (см. модель "плоский ротатор" в [3]).

Состояния, описываемые волновыми функциями типа Y_n,l,m, обычно называются чистыми. Кроме них существует множество состояний смешанных (или суперпозиционных), для которых одно или несколько квантовых чисел являются неопределенными:

Y_n,l = С₁(2р_–1) + С₂(2р₀) + С₃(2р₊₁)

Y_n = С₁(2s) + С₂(2р₊₁)

Y= С₁(1s) + С₂(2р₊₁)

Все такие функции, составленные из слагаемых с разными значениями квантовых чисел n и/или l, описывают нестационарные состояния, которые в течение короткого времени (порядка 10^–8 с) редуцируют к одному из стационарных состояний типа Y_n,l,m, в которых все три квантовые числа точно определены. Исключением из этого общего правила являются суперпозиционные функции типа Y_n,l. Редукция таких состояний может быть вызвана только действием внешних причин (например, магнитного поля).