Радиальная зависимость

Радиальная зависимость показывает характер изменения плотности электронного облака при перемещении вдоль радиуса r при постоянных значениях углов q и j. Такую зависимость можно описать различными способами. Первый из них заключается в использовании радиального множителя волновой функции либо в амплитудной форме R(r), либо в вероятностной форме |R(r)|².

Ниже приведены примерные графики некоторых радиальных зависимостей (шкала расстояний проградуирована в единицах а_о).

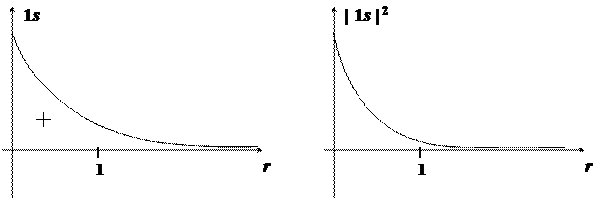
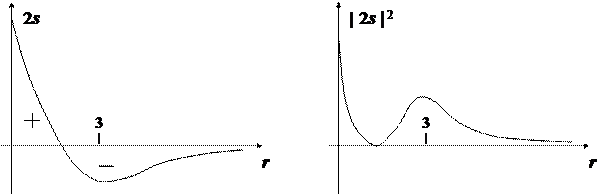
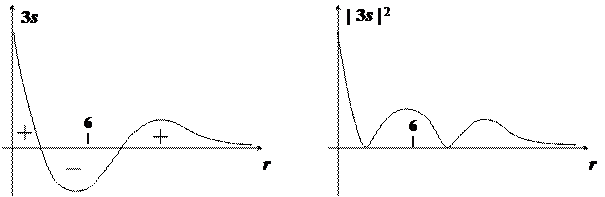
Из приведенных графиков легко заметить общую закономерность: для каждого типа функции ее первый представитель не имеет узлов. По мере возрастания главного квантового числа появляются узлы, и электронное облако оказывается разделенным на несколько не перекрывающихся между собой фрагментов. Так, например, для состояния 2s электронное облако состоит из двух частей, отделенных друг от друга сферической узловой поверхностью, а для состояния 3s — из трех частей, разделенных двумя узловыми поверхностями.

Для волновых функций других типов (р-, d- и т.д.) качественный вид графиков примерно такой же, что и для s-функций. Единственное существенное различие состоит в том, что графики этих функций начинаются из нулевой точки, т.е. при r = 0 и R(r) = 0, и, кроме того, узлы и максимумы расположены на других (бо́льших) расстояниях. В общем случае, радиальные части волновых функций для различных стационарных состояний атома водорода можно охарактеризовать числом узлов, которое определяется формулой: N_рад = n – l – 1.

Можно обратить внимание на то, что узловая структура и энергия электронных облаков не зависят от величины числа m. Так, например, для всех пяти состояний типа 3d число радиальных узлов равно нулю.

Иногда для описания радиальной зависимости используется т.н. "функция радиального распределения":

ФРР(r) = |R(r)|² × 4pr².

Она дает вероятность найти электрон на расстоянии r от ядра, независимо от углов, т.е. внутри тонкого шарового слоя, объем которого пропорционален 4pr². Графики ФРР существенно отличаются от графиков радиальных частей АО. Например, для состояния 1s функция R(r) имеет максимум на ядре и монотонно убывает по мере удаления от него. ФРР, напротив, имеет вблизи ядра минимум. Зато на ней имеется максимум на некотором расстоянии от ядра. Это связано с тем, что по мере удаления от ядра возрастает объем шарового слоя.

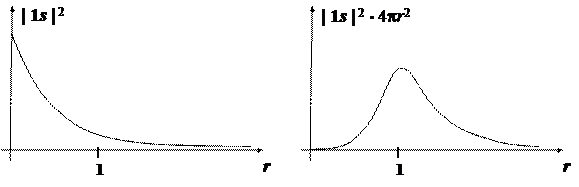
C физической точки зрения, это можно интерпретировать следующим образом. Плотность электронного облака для состояния 1s максимальна вблизи ядра. Однако доля объема облака в непосредственной близости от ядра чрезвычайно мала, и поэтому вероятность найти электрон на малых расстояниях невелика. Бо́льшую часть времени электрон проводит на расстояниях вблизи максимума ФРР. Для состояния 1s значение r, соответствующее этому максимуму, называется боровским радиусом (а_о) и используется в качестве единицы длины для структур атомных масштабов.