Угловая зависимость

Угловая зависимость показывает характер изменения электронной плотности при изменении углов q и j, но при некотором постоянном значении радиуса (r = const). Для изображения угловой зависимости также используются различные средства.

Во-первых, это графики шаровых функций Y(q, j) = Q(q) • F(j). Областью определения этих функций является поверхность сферы заданного радиуса. В каждой точке сферы, положение которой задано углами (q, j), можно построить стрелку, ориентированную перпендикулярно поверхности, и длина которой равна значению функции Y(q, j). В качестве конкретного примера можно проанализировать угловую часть функции 2р_z = cos q. Для большей наглядности рассмотрим только сечение сферы (области определения функции) по некоторому меридиану. Ясно, что вблизи полюсов функция будет иметь значение, близкое к 1 (при q = 0 cos q = 1). По мере приближения к экваториальной плоскости значение функции будет монотонно убывать, стремясь к нулю при q = 90° (символы + и – отражают знаки функции в верхней и нижней полусферах области определения).

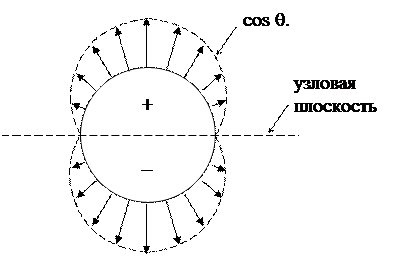
При переходе от одного значения радиуса к другому длины всех стрелок будут согласованно изменяться, в соответствии с величиной радиального множителя R(r), так что общий вид диаграммы полностью сохраняется. Такие графики можно несколько упростить, если все стрелки перенести в начало координатной системы.

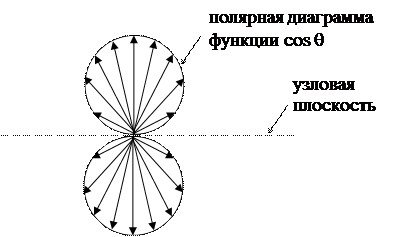
Для получения полной картины изображенное на рисунке плоское сечение необходимо повернуть вокруг вертикальной оси (z) на 360°. В результате получится поверхность вращения в виде двух одинаковых сфер, "надетых" на общую ось z. Подобные графики называются полярными диаграммами. Необходимо обратить внимание на то, что специфическая форма полярных диаграмм (например, "гантелеобразная" для функций типа 2р) отнюдь не отражает формы самого электронного облака. Электронное облако в любом случае заполняет весь объем околоядерного пространства и его форму правильнее считать сферической, несмотря на то, что плотность таких облаков (кроме s-AO) неодинакова в разных направлениях.

В ряде случаев можно ограничиться указанием только узловой структуры функции, не обращая внимания на длины стрелок. Такие максимально упрощенные графики угловых зависимостей будут иметь следующий вид (пунктиром обозначена область определения, сплошными линиями — узловые поверхности):

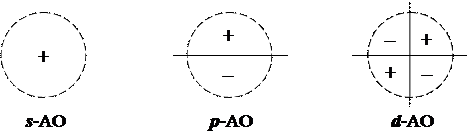
Из рисунка видно, что число узловых поверхностей углового типа растет пропорционально орбитальному квантовому числу: N_угл = l.

Следует подчеркнуть то обстоятельство, что у волновых функций имеется два типа узловых поверхностей: имеющие сферическую форму радиальные (N_рад = n – l – 1), которые электрон вынужден пересекать, двигаясь вдоль радиуса, и проходящие через ядро угловые (N_угл = l), которые электрон пересекает при движении по поверхности сферы.

Общее число узловых поверхностей для любой волновой функции определяется формулой: N = N_рад + N_угл = n – 1. Например, для функций 3s, 3p и 3d это число одинаково и равно 2, однако распределение узловых поверхностей по типам оказывается разным.

Это, в частности, свидетельствует о том, что переходы атома водорода, сопровождающиеся изменением орбитального квантового числа (типа s « p, s « d, p « d) не могут происходить самопроизвольно, несмотря на то, что полная энергия атома при таких переходах не изменяется.

Еще один способ описания электронного облака заключается в построении т.н. "изовероятных поверхностей" (ИВП), которые представляют собой графики функций |Y(r, q, j)|² = const. Константа задает некоторую величину плотности электронного облака. ИВП, следовательно, представляет собой поверхность, в любой точке которой вероятность обнаружения электрона одна и та же, независимо от углов и радиуса. Если построить ИВП для совокупности констант, мы получим набор таких поверхностей, вложенных друг в друга и дающих представление о распределении плотности облака в пространстве. Можно заметить, что частным случаем ИВП (при const = 0) являются узловые поверхности. Характерной особенностью ИВП является то, что их можно строить как для состояний, описываемых действительными функциями, так и для состояний с комплексными множителями. При возведении в квадрат комплексные множители типа exp(imj) дают единицу. Для таких состояний (с определенным значением проекции вектора L на ось z) ИВП лишены зависимости от угла j и всегда представляют собой поверхности вращения вокруг оси z. Наконец, можно отметить, что вместо совокупности ИВП часто используют только одну из них — такую, внутри которой заключена определенная доля (например, 90 или 95 %) всей электронной плотности облака.