Спин-орбитальное взаимодействие

Более детальное рассмотрение атома водорода позволяет установить еще одну его особенность. Она связана с тем обстоятельством, что механические моменты — орбитальный и спиновой — порождают соответствующие магнитные моменты. Эти два магнитных момента взаимодействуют между собой, влияя в результате на характер механического движения орбитального и спинового типов. Такой эффект носит название спин-орбитального взаимодействия (СОВ). Оно не учитывается в простой модели атома водорода, так как используемый в ней гамильтониан не содержит релятивистских членов, соответствующих магнитной энергии.

Для понимания смысла СОВ рассмотрим механическую модель: пусть имеются два гироскопа, вращающиеся вокруг некоторых осей. Каждый гироскоп характеризуется вектором механического момента: J₁ и J₂. В соответствии с общим механическим законом сохранения момента, величина обоих векторов, а также их проекции на любую пространственную ось не будут зависеть от времени:

| J₁ | = const, J_1z = const, | J₂ | = const, J_2z = const.

Если теперь связать гироскопы тонкой пружиной (или другой физической связью, например, магнитным полем), мы увидим, что оси вращения гироскопов уже не будут оставаться в покое, а начнут медленно вращаться вокруг некоторой общей оси. Угол между осями гироскопов при этом будет оставаться неизменным. Такое явление называется прецессией. Ясно, что в прецессирующей системе закон сохранения момента нарушается по отношению к каждому отдельному гироскопу: хотя длины векторов J₁ и J₂ сохраняются, их направления изменяются со временем. Однако, для объединенной системы, включающей оба связанных гироскопа, этот закон обязан выполняться — суммарный механический момент системы (J = J₁ + J₂) сохраняет и свою величину, и направление.

Таким образом, при наличии взаимодействия мы должны ввести новую величину: полный механический момент (J) , характеризуемый длиной | J | и одной из его проекций J_z. В результате, набор четырех характеристик системы, описывающих стационарное состояние, изменяется:

{ | J₁ |, | J₂ |, J_1z, J_2z } ¾® { | J₁ |, | J₂ |, | J |, J_z }

Совершенно аналогично выглядит ситуация с электроном в атоме водорода: в результате СОВ величины орбитального и спинового моментов остаются неизменными, но их ориентации в пространстве (т.е. проекции на ось z) перестают быть определенными. Вместо них следует ввести новую характеристику — полный механический момент атома (J= L + S), модуль которого | J | и проекция J_z являются строго определенными и сохраняющимися во времени величинами. Поскольку вектор полного механического момента по физическому смыслу полностью аналогичен векторам LиS, его параметры задаются аналогичными уравнениями:

| J |² = h²[ j(j + 1) ], где j — квантовое число полного механического момента электрона (аналог чисел l и s),

J_z = hm_j , где m_j— магнитное квантовое число полного механического момента (аналог чисел m_l и m_s).

Квантовое число j может быть рассчитано по такому правилу: максимальное значение числа j равно сумме чисел (l + s), а минимальное — модулю разности между ними |l – s|. Остальные значения располагаются между этими двумя крайними значениями с шагом 1. Для каждого значения числа j имеется (2j + 1) значение числа m_j = j, (j – 1), .... , (–j + 1), –j.

Например, пусть имеется электрон в состоянии 3d. Для него квантовые числа, определяющие длины орбитального и спинового моментов, имеют значения: l = 2 и s = 1/2. Тогда число j может иметь всего два допустимых значения: j = 2 + 1/2 = 5/2 и j = 2 – 1/2 = 3/2. Следовательно, сложение векторов L и S может привести только к двум результирующим векторам J. Первый вектор будет иметь длину:

| J | = h [ 5/2 (5/2 + 1)]^1/2 = h (35)^1/2/2

Вектор с таким модулем может иметь 2(5/2) + 1 = 6 проекций, определяемых значениями числа m_j = 5/2, 3/2, 1/2, –1/2, –3/2, –5/2.

Второй вектор будет иметь длину:

| J | = h [ 3/2 (3/2 + 1)]^1/2 = h (15)^1/2/2.

Вектор с таким модулем может иметь 2(3/2) + 1 = 4 проекции, определяемые значениями числа m_j = 3/2, 1/2, –1/2, –3/2.

Таким образом, набор пяти наблюдаемых (и нумерующих их квантовых чисел), определяющих стационарное состояние электрона, при учете СОВ заменяется другим набором:

Группы состояний, нумеруемые новыми квантовыми числами, имеют и новый тип обозначений. Эти обозначения состоят из центральной буквы, соответствующей величине числа l (s — для l = 0, р — для l = 1, d — для l = 2 и т.д.) и двух индексов. Верхний индекс равен т.н. мультиплетности 2s + 1, а нижний равен числу j. Так, например, рассмотренные выше состояния типа 3d будут обозначаться как

²d_5/2 ( 6 состояний, отличающихся величинами числа m_j),

²d_3/2 ( 4 состояния, отличающихся величинами числа m_j).

В заключение построим две ячеечные схемы, изображающие полные совокупности стационарных состояний атома водорода, которые широко используются для моделирования электронной структуры многоэлектронных атомов.

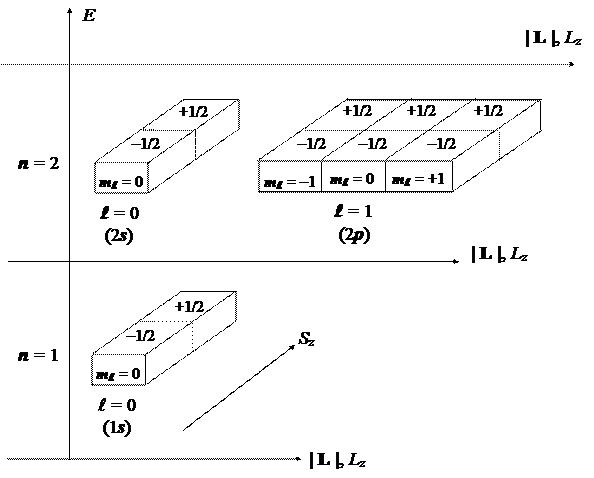
Здесь классификация стационарных состояний атома водорода производится без учета спин-орбитального взаимодействия, по наблюдаемым и квантовым числам, входящим в первый набор:

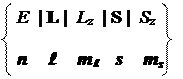
Вторая ячеечная схема описывает альтернативный способ классификации, с учетом спин-орбитального взаимодействия, в соответствии со вторым набором наблюдаемых и квантовых чисел:

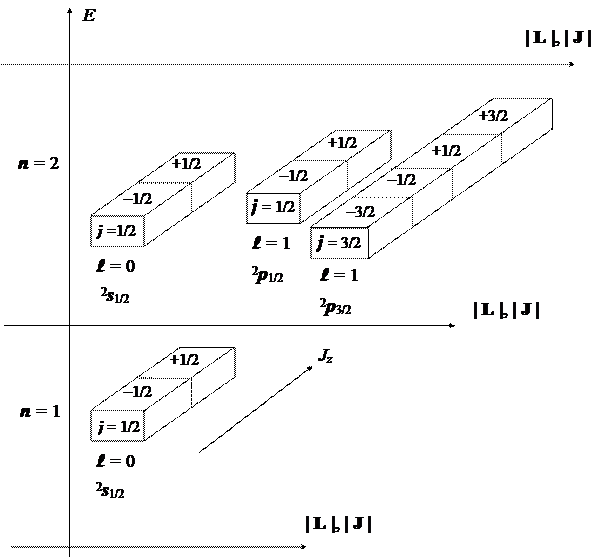
С некоторыми оговорками (в рамках т.н. "одноэлектронного приближения") обе эти схемы могут применяться для описания многоэлектронных атомов. В этом случае электроны распределяются по ячейкам-состояниям, в соответствии с определенными правилами (типа правил Клечковского, принципа Паули и т.д.).

Вопросы для самоконтроля

1. В чем смысл локального описания атома? Чем оно отличается от глобального?

2. Из каких частиц состоит атом? Каковы свойства этих частиц?

3. Какие межчастичные взаимодействия имеют место в атомах? В чем различие между релятивистской и нерелятивистской моделями атома?

4. Почему в квантовой химии обычно ограничиваются задачей описания только стационарных состояний атомов?

5. В каком базисе обычно представляют векторы состояния при описании атомов. Почему эти векторы необходимо изображать в функциональной форме — в виде волновых функций?

6. От каких переменных зависит волновая функция атома? Какова область определения волновых функций?

7. Каков физический смысл числовых значений пространственных множителей волновых функций атома?

8. Как решается задача определения явного вида волновых функций атома водорода?

9. Каков смысл квантовых чисел, используемых в описании атома водорода? Каковы их допустимые значения?

10. В чем различие между комплексными (КАО) и действительными (ДАО) волновыми функциями?

11. Можно ли, в соответствии с принципом суперпозиции, строить линейные комбинации из волновых функций атома водорода? Какие состояния атома описывают такие суперпозиционные функции?

12. Какие наблюдаемые входят в фундаментальный набор для атома водорода? Какова связь между значениями этих наблюдаемых и квантовыми числами?

13. Почему энергетические уровни атома водорода образуют систему, сходящуюся к определенному предельному значению энергии? Что происходит с атомом при достижении этого предельного значения?

14. Какова степень вырожденности энергетических уровней атома водорода?

15. Сколько значений может иметь модуль вектора орбитального момента при заданном значении энергии?

16. Сколько различных ориентаций может иметь вектор орбитального момента при заданном значении его модуля?

17. Дайте определение понятия "электронное облако". Почему точечную частицу — электрон — можно описывать моделью распределенного в пространстве "облака"?

18. Какие характеристики можно приписать электронному облаку?

19. Как можно вычислить плотность электронного облака в некоторой точке пространства?

20. Дайте определение понятия "узловая структура" электронного облака? В чем различие между радиальными и угловыми узловыми поверхностями? Как определить число узловых поверхностей каждого типа?

22. Как узловая структура связана со значениями наблюдаемых атома водорода — энергией и орбитальным моментом?

23. Какова связь между полярной диаграммой волновой функции и пространственной формой электронного облака?

23. Что такое "изовероятная поверхность"? В чем ее физический смысл?

24. Какие спиновые состояния доступны электрону в атоме водорода? С помощью каких наблюдаемых описываются эти состояния? Каковы допустимые значения этих наблюдаемых?

25. В чем различие между орбитальным и спиновым моментом электрона?

26. Какова причина спин-орбитального взаимодействия? К каким физическим последствиям приводит это взаимодействие?

27. Почему при учете спин-орбитального взаимодействия квантовые числа m_l и m_s необходимо заменять на j и m_j?