Атом с глобальной точки зрения

С глобальной точки зрения атом характеризуется набором механических наблюдаемых, т.е. таких величин, которые могут быть выражены числами, причем эти числа допускают, хотя бы в принципе, прямое экспериментальное измерение. Все глобальные наблюдаемые атома могут быть измерены с помощью стандартных экспериментальных процедур квантовой механики, основанных на применении спектральных анализаторов.

Первой в списке наблюдаемых стоит энергия. (Следует подчеркнуть, что речь здесь идет о внутренней энергии атома, которая не включает в себя ни кинетическую энергию движения атома как целого, ни потенциальную энергию атома во внешних полях, например, гравитационных.) Эту характеристику можно точно определить для любого объекта, находящегося в стационарном состоянии. Рассматривая атом как совокупность электронов, движущихся в потенциальной яме, созданной электрическим зарядом ядра, можно заключить, что атому доступно множество дискретных энергетических уровней. При действии различных возмущающих факторов (например, при электромагнитном облучении) атом может скачкообразно переходить из одного стационарного состояния в другое, поглощая или испуская дискретные порции (кванты) энергии. Дискретные энергетические уровни, соответствующие стационарным состояниям атома, называются атомными термами. Они могут быть обнаружены и исследованы различными экспериментальными средствами: ААС (атомная абсорбционная спектроскопия), АЭС (атомная эмиссионная спектроскопия), Оже-спектроскопия, ФЭС (фотоэлектронная спектроскопия) и т.д.

Список глобальных наблюдаемых атомов не исчерпывается одной энергией. Об этом свидетельствует ряд эффектов расщепления атомных термов под влиянием внешних полей — магнитных (эффекты Зеемана и Пашена-Бака) и электрических (эффект Штарка). Следовательно, одной и той же энергии (атомному терму) соответствует несколько состояний, различающихся значениями дополнительных характеристик. В качестве этих характеристик выступают механические моменты, порождаемые вращательным (орбитальным) движением электронов. Следует иметь в виду, что это движение отличается по своему характеру как от классического вращения, так и от элементарных квантовомеханических моделей типа плоского жесткого ротатора. Несмотря на это, многие важные особенности вращательного движения (например, способность тел, обладающих массой и электрическим зарядом, порождать момент импульса и магнитный момент) сохраняются и в этом случае.

Необходимо различать несколько разновидностей моментов. Во-первых, это полный механический момент атома (J), для которого можно определить модуль | J | и одну из проекций J_z :

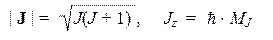
где J — квантовое число полного механического момента, а M_J — соответствующее магнитное число. Допустимые значения этих квантовых чисел для различных атомов задаются формулами:

J = 0, 1/2, 1, 3/2, 2, 5/2, … и M_J = –J, (–J + 1), …, (+J – 1), +J.

Поскольку электроны обладают электрическими зарядами, то с механическим моментом J всегда связан полный магнитный момент атома m_J, благодаря наличию которого атом может взаимодействовать с внешними магнитными полями. Следует иметь в виду, что, в отличие от элементарных частиц, для большинства атомов направление этого вектора не совпадает с направлением вектора механического момента: m_J ¹ g ×J. Несовпадение ориентаций двух векторов можно объяснить тем, что полный механический момента складывается из двух компонент: J = L +S,которые характеризуются аналогичными парами квантовых чисел:

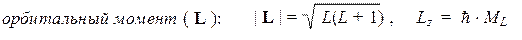
где: L = 0, 1, 2, 3, … и M_L = –L, (–L + 1), …, (+L – 1), +L ;

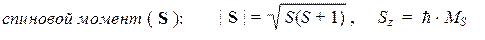
где: S = 0, 1/2, 1, 3/2, 2, … и M_S = –S, (–S + 1), …, (+S – 1), +S .

Каждый из этих моментов характеризуется своим магнитно-механическим отношением:

m_L = g_L ×Lи m_S = g_S ×S.

Поэтому в формуле, связывающей величины двух полных моментов — магнитного и механического, — имеется дополнительный множитель g, который называется "g-фактором" или "фактором Ланде" (в общем случае он представляет собой тензор 2 ранга):

m_J = g × g ×J

Полная энергия атома зависит от длин векторов J, L и S, но не от величин их проекций. Поэтому все состояния атома, которые характеризуются определенными значениями квантовых чисел J, L и S, имеют одну и ту же энергию. Совокупность таких вырожденных по энергии состояний атома также обозначается термином "атомный терм". Существует специальная номенклатура, в которой для обозначения атомных термов используют специальные символы, состоящие из буквы и двух числовых индексов:

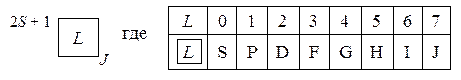
Например, символ ³Р₂ означает совокупность состояний атома, для которых квантовые числа имеют значения: J = 2, L = 1, S = 1. Между собой эти состояния различаются значениями магнитных чисел М_J, М_L и М_S.

Глобальные наблюдаемые атома не только доступны прямому экспериментальному измерению, но также могут быть вычислены как собственные значения соответствующих квантовомеханических операторов:

AY = A × Y

Для использования этих уравнений необходимо знать явный вид волновых функций Y, установление которых представляет собой центральную задачу теории физического атома.