Определение скорости точки плоской фигуры с помощью МЦС

Выберем за полюс точку Р. Тогда скорость произвольной точки А

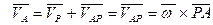, т.к.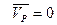

Таким образом, скорости точек тела при его плоском движении распределяются так же, как при вращательном движении тела вокруг неподвижной оси. Роль неподвижной оси играет мгновенная ось, проходящая через МЦС перпендикулярно плоской фигуре. Следовательно, скорости всех точек плоской фигуры перпендикулярны отрезкам, соединяющим эти точки с МЦС, а модули скоростей пропорциональны расстояниям от точек до МЦС

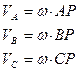(28)

Рис. 2.25

Определение угловой скорости плоской фигуры.

Угловая скорость плоской фигуры определяется одним единственным способом: она равна скорости любой точки плоской фигуры, деленной на расстояние от этой точки до МЦС:

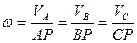(29)

Частные случаи определения положения МЦС.

1. МЦС находится в точке пересечения перпендикуляров с векторами скоростей двух точек плоской фигуры.

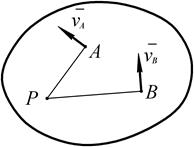
Рис. 2.26

2. Соединяем концы векторов. МЦС находится на пересечении линии, соединяющих концы векторов с линией АВ.

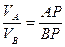
Рис. 2.27

3. ( 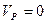, так как точки касания обоих тел при отсутствие скольжения должны иметь одинаковую скорость, а второе тело неподвижно)

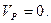
Рис. 2.28

4. 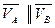, но 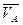не перпендикулярно АВ.

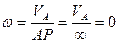
Согласно 2 способу определения скорости

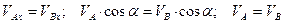
В данный момент времени скорости всех точек плоской фигуры геометрически равны. Имеем мгновенно поступательное

Рис. 2.29 распределение скорости. Угловая скорость равна нулю. МЦС находится в бесконечности.