Сложение ускорений. Теорема Кориолиса.
Найдем зависимость между абсолютным 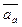 , относительным
, относительным 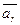 и переносным
и переносным 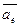 ускорениями. Эти величины отличаются не только тем, что при их вычислении рассматриваются приращения разных векторов скоростей, но и тем, что эти приращения вычисляются на разных перемещениях.
ускорениями. Эти величины отличаются не только тем, что при их вычислении рассматриваются приращения разных векторов скоростей, но и тем, что эти приращения вычисляются на разных перемещениях.
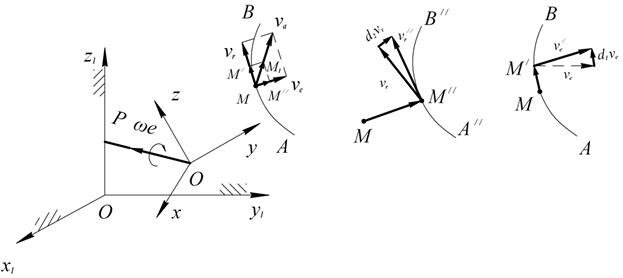
Рис. 2.16
При определении 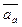 рассматривается приращение вектора
рассматривается приращение вектора 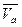 на абсолютном элементарном перемещении
на абсолютном элементарном перемещении 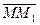 , при вычислении
, при вычислении 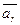 – приращении вектора
– приращении вектора 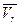 на относительном элементарном перемещении
на относительном элементарном перемещении 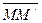 и при вычислении
и при вычислении 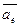 – приращение вектора
– приращение вектора  на переносном элементарном перемещении
на переносном элементарном перемещении 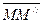 .
.
Условимся обозначать элементарное перемещение, получаемое вектором при абсолютном перемещении, символом d, при относительном – d1 и при переносном – d2. Тогда
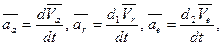 (*)
(*)
где 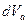 – элементарное приращение вектора
– элементарное приращение вектора 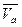 на абсолютном перемещении
на абсолютном перемещении 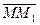 ,
,  – элементарное приращение вектора
– элементарное приращение вектора 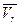 на абсолютном перемещении
на абсолютном перемещении 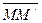 и
и  – элементарное приращение вектора
– элементарное приращение вектора  на абсолютном перемещении
на абсолютном перемещении 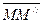 .
.
Поскольку при сложном движении 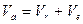 , то
, то
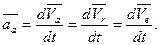
Однако в этом равенстве,  ,
,  как и
как и 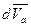 , представляют собой элементарные приращения соответственно векторов на абсолютном перемещении
, представляют собой элементарные приращения соответственно векторов на абсолютном перемещении 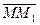 , поэтому стоящие справа величины не будут равны
, поэтому стоящие справа величины не будут равны 
Для получения искомых зависимостей учтем, что абсолютное перемещение 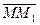 слагается геометрически из относительного и переносного элементарных перемещений
слагается геометрически из относительного и переносного элементарных перемещений 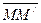 и
и 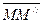 . Следовательно,
. Следовательно, 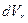 (элементарное приращение вектора
(элементарное приращение вектора 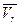 на абсолютном перемещении
на абсолютном перемещении 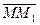 ) можно представить в виде
) можно представить в виде
 , (**)
, (**)
где  – элементарное приращение, получаемое вектором
– элементарное приращение, получаемое вектором 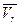 на относительном перемещении
на относительном перемещении 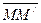 , а
, а  – элементарное приращение, получаемое тем же вектором на переносном перемещении
– элементарное приращение, получаемое тем же вектором на переносном перемещении 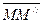 . Отношение
. Отношение  к
к 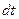 и дает согласно (*) величину
и дает согласно (*) величину  . Для вычисления
. Для вычисления  учтем, что переносное движение (движение осей О, х, у, z) слагается в общем случае из поступательного перемещения вместе с полюсом О и повороте вокруг мгновенной оси ОР, проходящей через этот полюс, угловую скорость этого поворота
учтем, что переносное движение (движение осей О, х, у, z) слагается в общем случае из поступательного перемещения вместе с полюсом О и повороте вокруг мгновенной оси ОР, проходящей через этот полюс, угловую скорость этого поворота 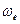 .
.
При поступательном перемещении вектор 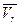 остается параллельным самому себе и никакого приращения не получает. При повороте нее вместе с осями О, х, у, z вокруг мгновенной оси ОР вектор
остается параллельным самому себе и никакого приращения не получает. При повороте нее вместе с осями О, х, у, z вокруг мгновенной оси ОР вектор 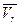 оставаясь постоянным по модулю, изменяет свое направление. Поворот вектора
оставаясь постоянным по модулю, изменяет свое направление. Поворот вектора 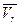 при непоступательном переносном движении и является причиной того, что этот вектор получает приращение
при непоступательном переносном движении и является причиной того, что этот вектор получает приращение 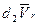 на перемещении
на перемещении 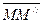 (рис. б, где
(рис. б, где 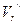 и А// В// изображают вектор
и А// В// изображают вектор 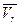 и кривую АВ в момент
и кривую АВ в момент  , а пунктиром показан вектор
, а пунктиром показан вектор 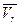 в момент
в момент 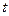 ). Приращение, получаемое вектором при таком повороте, определяется формулой
). Приращение, получаемое вектором при таком повороте, определяется формулой
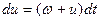 .
.
Следовательно, 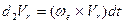 и
и 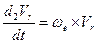 ,
,
где 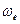 – угловая скорость переносного движения.
– угловая скорость переносного движения.
В результате из равенства (**) находим
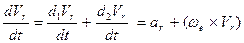 (А)
(А)
По аналогии с (**) величину 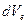 (элементарное приращение вектора
(элементарное приращение вектора  на абсолютном перемещении
на абсолютном перемещении 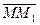 ) можно также представить в виде
) можно также представить в виде
 , (***)
, (***)
где 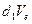 – элементарное приращение, получаемое вектором
– элементарное приращение, получаемое вектором  на относитель-ном перемещении
на относитель-ном перемещении 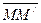 , а
, а  – элементарное приращение того же вектора на переносном перемещении
– элементарное приращение того же вектора на переносном перемещении 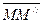 .
.
Согласно (*) 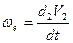 .
.
Скорость точки в случае плоскопоступательного движения ( 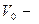 скорость полюса)
скорость полюса)
 (****)
(****)
Когда переносное движение не является поступательным (  ), значения
), значения  в точках М и М/ будут разными.
в точках М и М/ будут разными.
Вследствие этого вектор  на относительном перемещении
на относительном перемещении 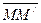 и получает приращение
и получает приращение 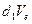 (см. рис в)
(см. рис в)  - значение
- значение  в точке М/, т.е в момент
в точке М/, т.е в момент  , а пунктиром показан вектор
, а пунктиром показан вектор  в точке М, т.е. в момент времени
в точке М, т.е. в момент времени 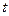 .
.
Чтобы найти 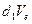 необходимо, продифференцировать равенство (****), считая в нем
необходимо, продифференцировать равенство (****), считая в нем 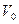 и
и 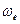 постоянными, а вектор
постоянными, а вектор 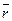 изменяется только в относительном движении.
изменяется только в относительном движении.
Тогда будем иметь:
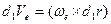 , где
, где 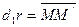
Следовательно
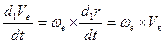
В результате из равенства (***) находим
 (В)
(В)
Найденные в ходе расчетов соотношения (А, В) показывают, что в общем случае производные 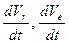 действительно отличаются от
действительно отличаются от  и
и  причем на одну и туже величину (
причем на одну и туже величину ( 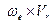 ).
).
Введем обозначение
 (25)
(25)
Величина, 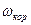 характеризующая изменения вектора относительной скорости
характеризующая изменения вектора относительной скорости  в переносном движении и вектора
в переносном движении и вектора  в относительном движении, называется поворотным или кориолисовым ускорением.
в относительном движении, называется поворотным или кориолисовым ускорением.
Окончательно получим
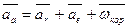 . (26)
. (26)
Формула выражает теорему Кориолиса: абсолютное ускорение точки равно геометрической сумме трех ускорений: относительного, характеризующего изменение относительной скорости точки в относительном движении, переносного, характеризующего изменение переносной скорости точки в переносном движении и кориолисова, характеризующего изменение относительной скорости в переносном движении и переносной скорости в относительном движении.
Если переносное движение поступательное, то 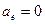 и
и  . Тогда
. Тогда  .
.
Направление  определятся по правилу векторного произведения. Кроме того, направление
определятся по правилу векторного произведения. Кроме того, направление 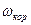 определяется по правилу Н.Е. Жуковского.
определяется по правилу Н.Е. Жуковского.
Чтобы определить направление вектора ускорения Кориолиса, следует вектор относительной скорости спроектировать на плоскость, перпендикулярную вектору угловой скорости переносного вращения, полученный при этом вектор следует повернуть в этой плоскости на угол 900 в сторону 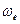 .
.

Рис. 2.17
Причины появления ускорения Кориолиса
Причиной появления ускорения Кориолиса является взаимное влияние относительного движения на переносное и переносного на относительное. В результате этого влияния переносная скорость меняет модуль и направление, а вектор относительной скорости – направление.
Пример
Пусть по радиусу диска, вращающегося вокруг оси, перпендикулярной плоскости диска, перемещается равномерно человек с относительной скоростью 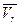 . Для какого-либо фиксированного момента времени
. Для какого-либо фиксированного момента времени 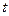
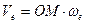 , то есть переносная скорость человека – скорость той точки диска, где в данный момент времени находится человек.
, то есть переносная скорость человека – скорость той точки диска, где в данный момент времени находится человек.
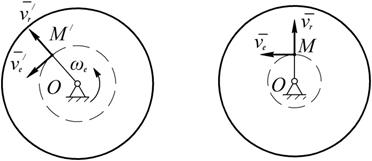
Рис. 2.18
Пусть в момент времени  человек занимает положение М/. Очевидно, что за время
человек занимает положение М/. Очевидно, что за время  относительная скорость изменяется по направлению от
относительная скорость изменяется по направлению от 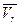 до
до 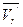 вследствие вращательного переносного движения. Вследствие относи-тельного движения человека из точки М в точку М/ модуль переносной скорости изменяется:
вследствие вращательного переносного движения. Вследствие относи-тельного движения человека из точки М в точку М/ модуль переносной скорости изменяется:
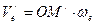
Указанные изменения вызывают появление Кориолисова ускорения.
Дата добавления: 2015-06-17; просмотров: 1316;
