Введение. Движение твердого тела называется плоским или плоскопараллельным, если все точки тела перемещаются в плоскостях

Рис. 2.19

Рассмотрим произвольное плоское движение твердого тела. Пусть все точки тела перемещаются в плоскостях, параллельных плоскостях Оху.

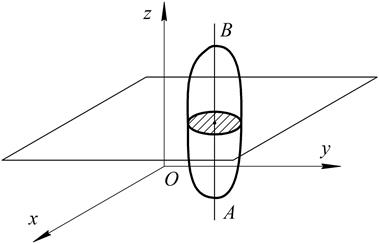
Рис. 2.20

Из определения плоского движения и из свойств твердого тела (углы между прямыми, фиксированными в твердом теле, сохраняются неизменными) следует, что любая прямая АВ, проведенная в теле перпендикулярна плоскости Оху, будет перемещаться поступательно, то есть траектории, скорости, ускорения всех точек этой прямой будут одинаковы.

Таким образом, для определения движения тела необходимо знать движение лишь одной точки на каждой прямой, проведенной перпендикулярно плоскости Оху. Взяв точки в одной плоскости, параллельно плоскости Оху, мы можем утверждать, что плоское движение твердого тела вполне определяется движением плоской фигуры, полученной от пересечения тела любой плоскостью, параллельной плоскости Оху.

Рис. 2.21

Свяжем жестко с плоской фигурой систему координат А,х,у. Тогда положение системы А,х,у, а вместе с ней и плоской фигуры относительно О,х₁,у ₁ будет определено заданием координат х_А,у_А точки А и углом 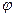между осями Ах₂ и Ах (оси Ах₂ и Ау₂ соответственно параллельно осям Ох₁ и Оу₁ и перемещаются при движении плоской фигуры поступательно).

Таким образом, определяют положение плоской фигуры в любой момент времени, то есть уравнения движения плоской фигуры.

5.2. Скорости точек тела при плоском движении.

Теорема.Скорость любой точки плоской фигуры равна геометрической сумме скорости точки, принятой за полюс и скорости данной точки при вращении плоской фигуры вокруг полюса.

Доказательство:

Рассмотрим плоскую фигуру. Точку А примем за полюс. Вычислим скорость точки В.

Радиус-вектор 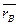– определяет положение точки В относительно 0х₁у₁.

Радиус-вектор 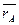– определяет положение точки А относительно 0х₁у₁.

Радиус-вектор 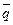– определяет положение точки В относительно 0х₂у₂.

Очевидно .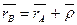

Продифференцируем по времени обе части записанного уравнения:

(*)

Заметим, что

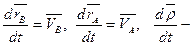скорость точки В относительно подвижной системы координат Ах₂у₂.

Введем обозначение .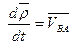

Движение тела относительно Ах₂у₂ представляет собой вращение тела вокруг оси Аz₂, перпендикулярно плоскости чертежа. Таким образом, 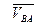– это скорость точки В при вращении тела вокруг оси, проходящей через полюс А, то есть с учетом формулы Эйлера.

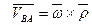
и равенство (*) примет вид

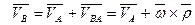(27)

Модуль скорости 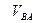определяется следующим образом:

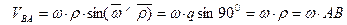
При этом вектор 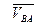перпендикулярен АВ ( ).

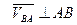Теорема. Проекции скоростей двух точек на прямую, их соединяющую, равны.

Рис. 2.23

Пусть скорость точки А известна – . Согласно предыдущей теореме для скорости точки В имеем .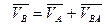

Спроектируем обе части этого равенства на ось х

, , так как 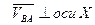, то есть .