Частные случаи определения МЦУ.

1. Известна точка, ускорение которой равно нулю. Эта точка и является МЦУ.

Например, качение без скольжения колеса по прямолинейному рельсу с постоянной скоростью центра С.

Так как 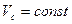, то 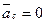, то есть точка С – есть МЦУ.

Ускорение любой точки, например В

;

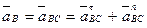Рис. 2.34 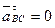, т.к. .

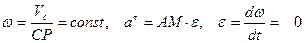Таким образом .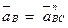

Ускорение каждой точки колеса направлено к МЦУ.

2. Равномерное вращение: .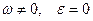

В этом случае

.

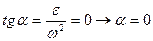Следовательно, ускорения всех точек направлены к МЦУ, причем расстояния от точки до МЦУ определяются по формуле

.

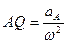Рис. 2.35

3. Момент, когда угловая скорость становится равной нулю:

В этом случае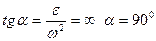

то есть ускорения всех точек направлены перпендикулярно к отрезкам, соединяющим эти точки с МЦУ.

Расстояние 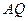вычисляется по формуле .

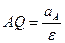Рис. 2.36

4. Момент времени, когда угловая скорость и угловое ускорение становится равным нулю при непоступательном движении твердого тела .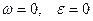

В этом случае ускорение любой точки равно ускорению полюса, то есть ускорения всех точек плоской фигуры геометрически равны

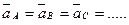
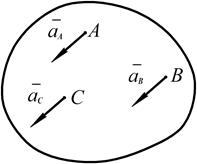
Рис. 2.37