Сложение вращений вокруг двух параллельных осей.
 Рассмотрим случай, когда относительное движение тела является вращением с угловой скоростью
Рассмотрим случай, когда относительное движение тела является вращением с угловой скоростью 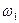 вокруг оси
вокруг оси 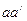 , укрепленный на кривошипе
, укрепленный на кривошипе 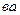 вокруг оси
вокруг оси 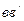 с угловой скоростью
с угловой скоростью 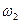 .
.
Если 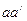 и
и 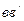 параллельны, то движение тела будет плоско-параллельным по отношению к плоскости, перпендикулярной осям.
параллельны, то движение тела будет плоско-параллельным по отношению к плоскости, перпендикулярной осям.
Исследуем отдельно случаи, когда вращения направлены в одну и в разные стороны.
Рис. 2.40
6.2.1. Вращения направлены в одну сторону.
 Изобразим сечение (S) тела, плоскостью, перпендикулярной осям. Следы осей в сечении (S) изображены буквами А и В. Легко видеть, что точка А, как лежащая на оси Аа/, получает скорость только от вращения вокруг оси Вв/, следовательно
Изобразим сечение (S) тела, плоскостью, перпендикулярной осям. Следы осей в сечении (S) изображены буквами А и В. Легко видеть, что точка А, как лежащая на оси Аа/, получает скорость только от вращения вокруг оси Вв/, следовательно 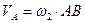 . Точно также
. Точно также 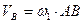 . При этом векторы
. При этом векторы 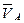 и
и 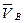 параллельны друг другу (оба перпендикулярны АВ) и направлены в разные стороны. Тогда точка С является МЦС (
параллельны друг другу (оба перпендикулярны АВ) и направлены в разные стороны. Тогда точка С является МЦС ( 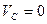 ), а следовательно ось Сс/, параллельна осям Аа/ и Вв/ является мгновенной осью вращения тела.
), а следовательно ось Сс/, параллельна осям Аа/ и Вв/ является мгновенной осью вращения тела.
Рис. 2.41
Для определения угловой скорости 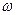 абсолютного вращения тела вокруг оси Сс/ и положения самой оси, т.е. точки С, воспользуемся равенством
абсолютного вращения тела вокруг оси Сс/ и положения самой оси, т.е. точки С, воспользуемся равенством
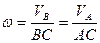 .
.
Из свойств пропорций получим
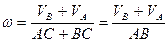
Подставляя 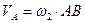 и
и 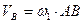 , получим:
, получим:
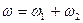 (34)
(34)
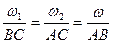 .
.
Итак, если тело участвует одновременно в двух направленных в одну сторону вращениях вокруг параллельных осей, то его результирующее движение будет мгновенным вращением с абсолютной угловой скоростью 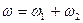 вокруг мгновенной оси, параллельной данной.
вокруг мгновенной оси, параллельной данной.
С течением времени мгновенная ось вращения Сс/ будет менять свое положение, описывая цилиндрическую поверхность.
6.2.2. Вращения направлены в разные стороны.
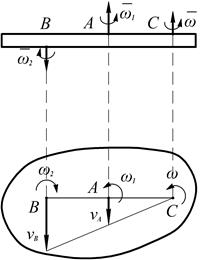
Рис. 2.42
Допустим для определения 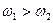 . Рассуждая, как и в предыдущем случае
. Рассуждая, как и в предыдущем случае
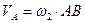
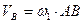
При этом 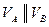 и направлены в одну сторону.
и направлены в одну сторону.
Тогда мгновенная ось вращения проходит через точку С, причем
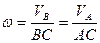 ,
,
или свойствам пропорций
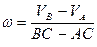
Подставляя значения 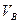 и
и 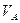 , получим
, получим
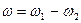 (35)
(35)
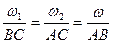
Итак, в этом случае результирующее движение также является мгновенным вращением с абсолютной угловой скоростью 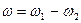 вокруг оси Сс/, положение которой определяется пропорцией
вокруг оси Сс/, положение которой определяется пропорцией
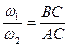 .
.
Дата добавления: 2015-06-17; просмотров: 1020;
