Сложение вращений вокруг пересекающихся осей.

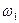Рассмотрим случай сложения вращения вокруг двух пересекающихся осей. Когда абсолютное движение тела является результатом относительного и переносного вращений с угловыми скоростями и 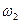вокруг осей О и Ов, пересекающихся в точке О, то скорость точки О, очевидно равна нулю.

Следовательно, результирующие движения тела является движением вокруг неподвижной точки О и для каждого элементарного

Рис. 2.45 промежутка времени представляет собой элементарный поворот с угловой скоростью 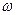вокруг мгновенной оси, проходящей через точку О.

Чтобы определить вектор 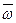, вычислим скорость какой-нибудь точки М тела, радиус-вектор которой 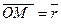. В относительном движении вокруг оси Оа точка М получает скорость 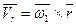, в переносном же движении вокруг оси Ов точка получает скорость .

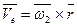Следовательно, абсолютная скорость точки М равна

.

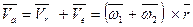С другой стороны, так как результирующие движение тела является мгновенным вращением с некоторой угловой скоростью 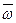, то должно быть .

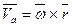Такие результаты будут получаться для всех точек тела (т.е. при любых ).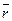

Отсюда заключаем, что

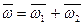. (36)

Следовательно, при сложном вращении вокруг двух осей, пересекающихся в точке О, результирующие движение будет мгновенным вращением вокруг оси Ос, проходящей через точку О, причем угловая скорость 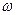этого вращения равна геометрической сумме относительной и переносной угловых скоростей.

С течением времени ось Ос меняет свое положение, описывая коническую поверхность, вершина которой находится в точке О.

Если тело участвует одновременно в мгновенных вращениях вокруг нескольких осей, пересекающихся в точке О, то последняя применяя полученное равенство ( 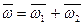), придем к выводу, что результирующие движение является мгновенным вращением вокруг оси, проходящей через точку О, а угловая скорость этого движения

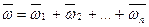. (37)