Сложение поступательного и вращательного движений.

6.5.1. Скорость поступательного движения перпендикулярно к оси вращения ( ┴ )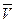

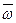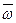Пусть сложное движение тела слагается из вращательного движения вокруг оси Аа с угловой скоростью и поступательного движения со скоростью 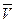перпендикулярно к .

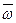Можно видеть, что движение представляет собою (по отношению к плоскости, перпендикулярно к оси Аа) плоскопараллельное движение. Если считать точку А полюсом, то рассматриваемое движение, как и

Рис. 2.46 всякое плоскопараллельное, будет действительно слагаться изпоступательного со скоростью 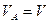, т.е со скоростью полюса и вращательного вокруг оси Аа, проходящей через полюс.

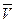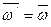Вектор можно заменить парой угловых скоростей (пара вращений), беря , а 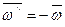. При этом расстояние АР найдется из равенства 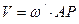с учетом, что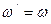

Векторы 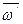и 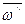дают при сложении нуль, и мы получаем, что движение тела в этом случае можно рассматривать как мгновенное вращение вокруг оси Р_р с угловой скоростью 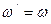. Точка Р для сечения (S) тела является МЦС ( ).

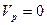Поворот тела вокруг осей А_а и Р_р происходит с одной и той же угловой скоростью 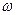, т.е. вращательная часть движения не зависит от выбора полюса.

6.5.2. Винтовое движение ( ).

Сложное движение слагается из вращательного вокруг оси А_а с угловой скоростью 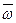и поступательного со скоростью 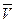, направленной параллельно оси А_а. Такое движение называется винтовым. Ось А_а называется осью винта.

Когда векторы 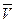и 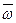направлены в одну сторону, то винт будет правым; если в разные стороны – левым.

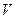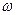Расстояние, проходимое за время одного оборота любой точки, лежащей на оси винта, называется шагом h винта. Если величины и постоянны, то шаг винта также будет постоянным. Обозначая время одного оборота через Т, получим 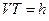и , откуда .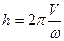

.

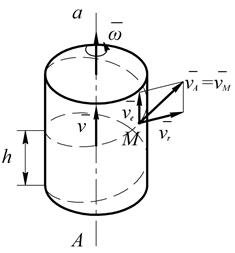
Рис. 2.46

При постоянном шаге любая точка М тела, не лежащая на оси винта, описывает винтовую линию. Скорость точки М, находящейся от оси винта на расстоянии r, складывается из поступательной скорости 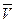и перпендикулярной к ней скорости 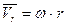, получаемой во вращательном движении. Следовательно

.

Направлена скорость 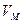по касательной к винтовой линии.

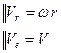(38)

6.5.3. Скорость поступательного движения образует произвольный угол с осью вращения.

Сложное движение, совершаемое телом в этом случае, представляет

собой общий случай движения свободного твердого тела.

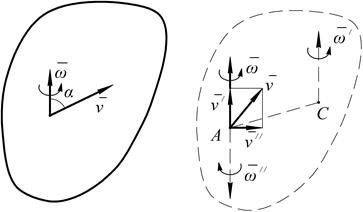
Рис. 2.48

Разложим вектор 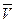на составляющие:

1). 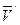, направленную вдоль .

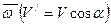2). 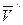, перпендикулярную к .

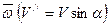Скорость 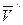можно заменить парой угловых скоросте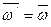й и 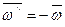, после чего векторы 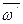и 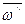можно отбросить. расстояние АС найдем по формуле:

.

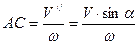Тогда у тела остается вращение с угловой скоростью 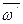и поступательное движение со скоростью 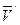. Следовательно, распределение скоростей точек тела в данный момент времени будет таким же, как при винтовом движении вокруг оси С_с с угловой скоростью 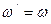и поступательной .

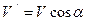Проделанными операциями мы перешли от полюса А к полюсу С. Результат показывает, что в общем случае движения угловая скорость тела при перемене полюса не изменяется ( 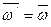), а меняется только поступательная скорость ( ).

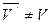Поскольку при движении свободного твердого тела величины

будут вообще все время меняться и положение оси С_с, которую поэтому называют мгновенной винтовой осью. Таким образом, движение свободного твердого тела можно еще рассматривать как слагающееся из серии мгновенных винтовых движений вокруг непрерывно изменяющихся винтовых осей.