ТЕМА 10. ОЦЕНКА СТОИМОСТИ АКЦИЙ

Долевыми ценными бумагами являются различные виды акций. Как и в случае с облигациями, различают несколько количественных ха­рактеристик, используемых для оценки акции: внутренняя, номиналь­ная, балансовая, конверсионная и ликвидационная стоимости, а так­же эмиссионная и курсовая цены.

Как и в случае с облигациями, внутренняя стоимость представля­ет собой расчетный показатель.

Конверсионную стоимость можно рассчитывать для привилеги­рованных акций, в условиях эмиссии которых предусмотрена возмож­ность их конвертации в обыкновенные акции.

Номинальная стоимость акции — это стоимость, указанная на блан­ке акции. В отличие от облигации, для которой номинальная стоимость имеет существенное значение, поскольку проценты по облигациям устанавливаются по отношению к номиналу независимо от курсовой цены, для акции этот показатель практически не имеет значения и несет лишь информационную нагрузку, характеризуя долю уставного капи­тала, которая приходилась на одну акцию в момент учреждения ком­пании.

Эмиссионная цена представляет собой цену, по которой акция эми­тируется, т.е. продается на первичном рынке. Эта цена может отли­чаться от номинальной стоимости, поскольку чаще всего размещение акций производится через посредническую фирму, являющуюся про­фессиональным участником фондового рынка. В этом случае посред­ническая фирма скупает весь выпуск акций по согласованной цене и в дальнейшем реализует их на рынке по цене, которая определяется уже этой фирмой и, естественно, превышает номинал.

С началом операций компании доля капитала, приходящаяся на одну акцию, немедленно меняется. С этой точки зрения акция харак­теризуется балансовой стоимостью, которая может быть рассчитана по балансу как отношение стоимости чистых активов (общая стоимость активов по балансу за минусом задолженности кредиторам) к общему числу выпущенных акций.

Ликвидационная стоимость акции может быть определена лишь в момент ликвидации общества. Она показывает, какая часть стоимос­ти активов по ценам возможной реализации, оставшаяся после расче­тов с кредиторами, приходится на одну акцию. Поскольку учетные цены активов могут значительно отличаться от их рыночных цен в зависимости от инфляции и конъюнктуры рынка, ликвидационная сто­имость не равна балансовой.

Для учета и анализа наибольшее значение имеет курсовая (теку­щая рыночная) цена. Именно по этой цене акция котируется (оце­нивается) на вторичном рынке ценных бумаг. Курсовая цена зави­сит от разных факторов: конъюнктуры рынка, рыночной нормы при­были, величины и динамики дивиденда, выплачиваемого по акции, и др. Она может определяться различными способами, однако в основе их лежит один и тот же принцип — сопоставление дохода, приносимого данной акцией, с рыночной нормой прибыли. В ка­честве показателя дохода можно использовать либо дивиденд, либо величину чистой прибыли, приходящейся на акцию. Более оправ­данным является использование дивиденда, однако в некоторых случаях, например, компания находится в стадии становления или крупной реорганизации, когда значительная часть чистой прибыли реинвестируется, использование показателя чистой прибыли на акцию позволяет получить более реальную оценку экономической ситуации.

Оценка целесообразности приобретения акций, как и в случае с облигациями, предполагает расчет теоретической стоимости акции и сравнение ее с текущей рыночной ценой.

Привилегированные акции, как и бессрочные облигации, генери­руют доход неопределенно долго, поэтому их текущая теоретическая стоимость определяется по формуле. Таким образом, наиболее простым вариантом оценки привилегированной акции является от­ношение величины дивиденда к рыночной норме прибыли по акци­ям данного класса риска (например, ставке банковского процента по депозитам с поправкой на риск).

В некоторых странах привилегированные акции нередко эмити­руются на условиях, позволяющих эмитенту выкупить их в опреде­ленный момент времени посоответствующей цене, называемой це­ной выкупа (call price). В этом случае текущая теоретическая сто­имость таких акций определяется по формуле, где М заменяется ценой выкупа Р_с Эмиссия бессрочных привилегированных акций, предусматривающих выплату дивиденда по постоянной ставке, является довольно рисковым мероприятием, поскольку невозможно спрогнозировать процентные ставки на длительную перспективу. Именно поэтому условиями выпуска привилегированных акций нередко принимается во внимание их конверсия в обыкновенные акции.

Что касается обыкновенных акций, то известны различные ме­тоды их оценки; наиболее распространенным из них является метод, основанный на оценке их будущих поступлений. В зависимости от предполагаемой динамики ди­видендов конкретное представление формулы меняется. Ба­зовыми являются три варианта динамики прогнозных значений дивидендов:

дивиденды не меняются (ситуация аналогична ситуации с приви­легированными акциями, т.е. применяется формула);

дивиденды возрастают с постоянным темпом прироста;

дивиденды возрастают с изменяющимся темпом прирост.

1. Оценка акции с равномерно возрастающими дивидендами

Предполагается, что базовая величина дивиденда (т.е. последнего выплаченного дивиденда) равна С; ежегодно она увеличивается с тем­пом прироста g. Например, по окончании первого года периода про­гнозирования будет выплачен дивиденд в размере С•( ] + g) и т.д. Тог­да формула имеет вид:

,

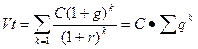где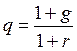

Домножив обе части на q и вычтя новое уравнение из (8.6), получим: V_t • (1 - q) = С • g. Таким образом:

, (8.7)

Данная формула имеет смысл при г > g и называется моделью Гор­дона. Отметим, что показатели rи g в этой и последующих формулах берутся в долях единицы. Очевидно, что числитель формулы пред­ставляет собой первый ожидаемый дивиденд фазы постоянного роста.

2. Оценка акций с изменяющимся темпом прироста

Из формулы видно, что текущая цена обыкновенной акции очень чувствительна к параметру g. Даже незначительное его изме­нение может существенно повлиять на цену. Поэтому в расчетах иногда пытаются разбить интервал прогнозирования на подынтер­валы, каждый из которых характеризуется собственным темпом при­роста g. Так, если выделить два подынтервала с темпами прироста g и р соответственно, то формула принимает вид:

,

где С₀ — дивиденд, выплаченный в базисный момент времени;

С_k — прогноз дивиденда в к-м периоде;

g — прогноз темпа прироста дивиденда в первые к подпериодов;

р _ прогноз темпа прироста дивидендов в последующие подпериоды.

Главная сложность этой модели состоит в выделении подперио­дов, прогнозировании темпов прироста (как правило, в прогнозах тем­пы прироста в динамике снижаются) и коэффициентов дисконтиро­вания для каждого подпериода. При выделении нескольких подпери­одов модель становится более громоздкой в представлении, однако вычислительные процедуры достаточно просты. Безусловно, модель должна рассматриваться в динамике и постоянно уточняться по мере получения новой информации, в частности по истечении очередного подпериода.

В теории и практике оценки акций описана и получила достаточ­но широкое распространение ситуация, когда темп прироста диви­дендов в течение нескольких лет прогнозного периода меняется (фаза непостоянного роста), однако по истечении этих лет он устанавли­вается на некотором постоянном уровне. Считается, что такое разви­тие событий характерно для компаний, находящихся в стадии ста­новления, либо уже зрелых компаний, осваивающих новые виды продукции или перспективные рынки сбыта. Тогда в течение непро­должительного подпериода темп прироста может быть сравнитель­но высоким, причем не обязательно одинаковым, а затем он снижа­ется и становится постоянным. Наиболее общая постановка задачи в этом случае такова.

Пусть продолжительность фазы непостоянного роста составляете лет, дивиденды в этот период по годам равны С _j , j= 1,2,..., к. С_л+1 — первый ожидаемый дивиденд фазы постоянного роста с темпом g; r — приемлемая норма прибыли. В первые к лет прогнозируется бессистемное изменение величины годового дивиденда, а начиная с момента (к + /), эта величина равномерно увеличивается, т.е.

С_к+1 ⁼ Ck • (1 + g); С_к+2= С_к+1 • (1 + g) = Ck • (1+g)² и т.д.

Тогда второе слагаемое будет иметь вид:

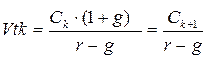
Показатель Vtk дает оценку акции на конец периода к. Поскольку мы пытаемся сделать оценку с позиции начала первого года, значение Vtk нужно дисконтировать. Таким образом, формула (8.8), позволяю­щая рассчитать теоретическую стоимость акции на конец года 0, мо­жет быть трансформирована следующим образом;

Пример. В течение последующих четырех лет компания планирует выпла­чивать дивиденды соответственно 1,5; 2; 2,2; 2,6 долл. на акцию. Ожи­дается, что в дальнейшем дивиденд будет увеличиваться равномерно с темпом 4% в год. Рассчитать теоретическую стоимость акции, если рыночная норма прибыли 12%.

Величина ожидаемого дивиденда пятого года будет равна: 2,6 * 1,04 = 2,7 долл. По формуле:

Таким образом, в условиях эффективного рынка акции данной ком­пании на момент оценки должны продаваться по цене, примерно рав­ной 27,62 долл.