ТЕМА 12. ПОКАЗАТЕЛИ ОЦЕНКИ РИСКА
Доход, обеспечиваемый каким-либо активом, состоит из двух компонентов — полученных дивидендов и дохода от изменения стоимости актива. Доход, исчисленный в процентах к первоначальной стоимости актива, называется доходностью данного актива, или нормой прибыли. Доход — это абсолютный показатель, его можно суммировать в пространстве и времени (в данном случае пока не учитывается временная стоимость денег); доходность — показатель относительный и такого суммирования делать уже нельзя.
Пример
Предприниматель год назад приобрел акцию предприятия по цене 15 руб. Текущая рыночная цена акции — 16,7 руб., полученные дивиденды составили 1 руб. Тогда суммарный доход равен 2,7 руб., а общая доходность данного вида активов для предпринимателя составляет:
к = (1 +(16,7- 15,0))/ 15,0 = 0,18, или 18%.
Финансовые менеджеры, по возможности, пытаются учитывать риск в своей работе. При этом появляются различные варианты поведения, а значит, и типы менеджера в зависимости от склонности к риску. Однако ключевая идея, которой руководствуется менеджер, заключается в следующем: требуемая (или ожидаемая) доходность и риск изменяются в одном направлении, т.е. пропорционально друг другу.
Совершенно очевидно, что, поскольку риск является вероятностной оценкой, его количественное измерение не может быть однозначным и предопределенным. Более того, проблема оценки риска финансовых активов многоаспектна как с позиции методов оценки, так и с позиции стратегии и тактики управления этими активами.
Количественно риск может быть охарактеризован как некий показатель, измеряющий вариабельность дохода или доходности. Таким образом, первый и очевидный вывод состоит в том, что, как показано в курсе экономической статистики, для этой цели можно использовать ряд статистических коэффициентов, в частности:
• ожидаемая доходность;
• стандартное отклонение;
• коэффициент вариации.
Ожидаемая доходность по каждому активу - одна из важнейших характеристик эффективности инвестиций. Для ее расчета используется следующая формула

где r – один из возможных исходов
Pi – вероятность наступления исхода i
i – общее число возможных исходов.
То есть ожидаемая доходность актива рассчитывается как, средневзвешенная доходностей при разных будущих состояниях экономики по вероятности наступления этих будущих состояний. Очевидно, что наиболее предпочтительные проекты обладают наибольшей ожидаемой доходностью. Рассчитанная таким образом ожидаемая доходность не является той величиной, которая будет достигнута. Эта величина может рассматриваться как наиболее вероятная или как математическое ожидание доходностей при различных будущих состояниях экономики.
Стандартное отклонение σ или корень из дисперсии рассчитывается по следующей формуле:
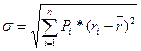
Данная характеристика является наиболее распространенной для численной оценки риска. Очень часто стандартное отклонение и называют риском (почти всегда при финансовых инвестициях). Отметим, что данный показатель позволяет оценить отклонения величин доходности от ожидаемого значения. Соответственно, чем меньше разброс значений доходности при различных состояниях экономики, тем меньшим уровнем риска будет характеризоваться данный актив. Необходимо понимать, что использование стандартного отклонения или дисперсии как меры риска предполагает нормальное распределение доходности, иными словами, значения доходностей актива при разных состояниях экономики должны быть симметричны относительно ожидаемой доходности. В противном случае использование данных показателей для оценки риска является нецелесообразным, так как даст неверный результат.
Все вышеприведенные показатели обладают одним общим недостатком — это абсолютные показатели, значение которых существенно зависит от абсолютных значений исходного признака ряда. Поэтому большее применение имеет коэффициент вариации.
Известно, что уровень риска и величина доходности в большинстве случаев находятся в прямой зависимости, т. е. увеличение доходности возможно при соответствующем увеличений риска активы, и наоборот. Но мера риска является величиной условной и относительной, поэтому может так оказаться, что некоторые проекты обладают одинаковым риском, рассчитанным по одному из двух предложенных методов. В этом случае для оценки риска используется показатель коэффициента вариаций V, который рассчитывается как отношение стандартного отклонения к ожидаемой доходности:
V = σ / 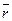
Из нескольких альтернативных активов, предпочтение отдается тому активу, который имеет наименьший коэффициент вариации, т.е. имеет наименьший уровень риска на единицу доходности.
В отношении оценки риска финансовых активов необходимо сделать три замечания. Во-первых, как отмечалось выше, количественно риск может оцениваться вариабельностью либо дохода, либо доходности. Поскольку доход в абсолютной оценке может существенно варьировать при сравнительном анализе различных финансовых активов, то принято в качестве базисного показателя, характеризующего результативность операции с финансовым активом, использовать не доход, а доходность. Очевидно, что, вложив ту или иною сумму денежных средств в акции, можно получать разный доход по абсолютной величине, однако доходность не зависит от размера инвестиции и потому сопоставима в пространственно-временном разрезе.
Во-вторых, основными показателями оценки риска на рынке капитала являются дисперсия и среднее квадратическое отклонение. Распространенность и пригодность в сравнительном анализе этих статистик в данном случае объясняется тем обстоятельством, что базисным показателем при расчетах является доходность, т.е. относительный показатель, сопоставимый как в динамике, так и по различным видам активов. Поэтому независимо от анализируемых активов соответствующие им показатели доходности и дисперсии однопорядковы, и нет острой необходимости применять в оценке коэффициент вариации.
В-третьих, приведенные формулы рассчитаны на дискретные ряды, В приложении к финансовым активам они могут применяться в ретроспективном анализе. Однако, как уже неоднократно подчеркивалось, при работе на рынке капитала гораздо более ценен перспективный анализ, в рамках которого большинство величин, представляющих интерес для инвестора, оценивается в вероятностных терминах, Именно поэтому при оценке риска используют модификации формул (9.2) и (9.3), в которых весами значений ожидаемой (или требуемой) доходности являются вероятности их появления. Ниже будут приведены соответствующие формулы для расчета.
Необходимо отметить еще одну очень важную особенность анализа риска и доходности. Как и любая вероятностная категория, риск может быть оценен по-разному Однако речь должна идти не только и не столько о различии в алгоритмах и критериях оценки, приведенных выше, сколько о том, рассматривается ли данный финансовый актив изолированно или как составная часть набора активов. Эта проблема будет рассмотрена в следующем разделе.
При рассмотрении актива изолированно никаких особых проблем теоретического характера в принципе не возникает, а его рисковость может быть измерена с помощью одной из рассмотренных выше статистик. Тем не менее, как и в любом перспективном анализе, инвестор в этом случае сталкивается с одной проблемой, а именно с проблемой оценки ожидаемых значений исходных параметров. В частности, какой бы мерой инвестор ни пользовался, ему необходимо оценить ожидаемую доходность актива. Чаще всего делают три оценки: пессимистическую, наиболее вероятную и оптимистическую. Безусловно, число исходов может быть увеличено, однако степень разумной достоверности ожидаемых значений доходности и вероятностей их осуществления при этом, естественно, снизится.
Задача. Рассчитать показатели риска активов А и В, если известна следующая информация:
Таблица – Вероятностные распределения доходности акций А и В.
| спрос | вероятность | Доходность акций, % | |
| А | В | ||
| Высокий | 0,3 | ||
| Средний | 0,4 | ||
| Низкий | 0,3 | -70 |
Ответить на вопрос, какой актив является наиболее предпочтительным для инвестирования?
Решение:
1) на первом этапе рассчитываем ожидаемую доходность активов А и В:
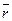 А = 0,3*100+0,4*15+0,3(-70)=30+6-21=15
А = 0,3*100+0,4*15+0,3(-70)=30+6-21=15
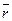 В = 0,3*20+0,4*15+0,3*10=6+6+3=15
В = 0,3*20+0,4*15+0,3*10=6+6+3=15
2) на втором этапе рассчитываем стандартное отклонение актива А и В
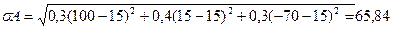
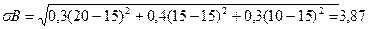
σA >σB
3) Далее рассчитываем коэффициент вариации активов А и В
VA = 65.84/15=4.39
VB = 3.87/15=0.26
Вывод по задаче: предпочтительней является актив В т.к. коэффициент вариации принимает минимальное значение.
Дата добавления: 2015-06-05; просмотров: 2295;
