Оценка аннуитета

Одним из ключевых понятий в финансовых и коммерческих рас­четах является понятие аннуитета. Логика, заложенная в схему анну­итетных платежей, широко используется при оценке долговых и доле­вых ценных бумаг, в анализе инвестиционных проектов, а также в ана­лизе аренды.

3.1 ОЦЕНКА СРОЧНЫХ АННУИТЕТОВ

Аннуитет представляет собой частный случай денежного потока. Известны два подхода к его определению. Согласно первому подходу аннуитет представляет собой однонаправленный денежный поток, элементы которого имеют место через равные временные интервалы. Второй подход накладывает дополнительное ограничение, а именно элементы денежного потока одинаковы по величине. В дальнейшем изложении материала мы будем придерживаться именно второго под­хода. Если число равных временных интервалов ограничено, аннуи­тет называется срочным. В этом случае

C₁ = C₂ = … = C_n = A.

Как и в общем случае, выделяют два типа аннуитетов: постнумерандо и пренумерандо (рис. 6).

Рис. 6Виды срочных аннуитетов

Примером срочного аннуитета постнумерандо могут служить ре­гулярно поступающие рентные платежи за пользование сданным в аренду земельным участком в случае, если договором предусматри­вается регулярная оплата аренды по истечении очередного периода. В качестве срочного аннуитета пренумерандо выступает, например, схема периодических денежных вкладов на банковский счет в начале каждого месяца с целью накопления достаточной суммы для круп­ной покупки.

Исторически вначале рассматривались ежегодные (период равен одному году) денежные поступления, что и послужило основой для названия «аннуитет» (так как год на латинском языке — anno). В даль­нейшем в качестве периода стал выступать любой промежуток време­ни при сохранении прежнего названия. Аннуитет еще называют фи­нансовой рентой, или просто рентой. Любое денежное поступление называется членом ренты, а величина постоянного временного ин­тервала между двумя последовательными денежными поступления­ми называется периодом аннуитета (периодом ренты).

Для оценки будущей и приведенной стоимости аннуитета можно пользоваться рассмотренными формулами, вместе с тем благодаря специфике аннуитетов в отношении равен­ства денежных поступлений эти формулы могут быть существенно упрощены.

Прямая задача оценки срочного аннуитета при заданных величи­нах регулярного поступления (А) и процентной ставке (r) предполага­ет оценку будущей стоимости аннуитета. Как следует из логики, при­сущей схеме аннуитета постнумерандо, наращенный денежный поток имеет вид:

А · (1 + r)^n-1, А · (1 + r)^n-2 , ... , А · (1 + r), А,

а формула трансформируется следующим образом:

.

Входящий в формулу множитель FM3(r, n) называется мультипли­цирующим множителем для аннуитета, или коэффициентом нара­щения ренты (аннуитета), и представляет собой сумму п первых членов геометрической прогрессии, начинающейся с 1, и знаменателем (1 + r).

Таким образом,

.

Экономический смысл мультиплицирующего множителя FM3(r, n) заключается в следующем: он показывает, чему будет равна суммар­ная величина срочного аннуитета в одну денежную единицу.

.

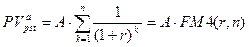Множитель FM4(r,n) называется дисконтирующим множителем для аннуитета, или коэффициентом дисконтирования ренты (аннуитета), и как сумма членов геометрической профессии равен величине:

.

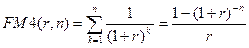Экономический смысл дисконтирующего множителя FM4(r, n) зак­лючается в следующем: он показывает, чему равна с позиции текущего момента величина аннуитета с регулярными денежными поступлени­ями в размере одной денежной единицы (например, один рубль), продолжающегося п равных периодов с заданной процентной ставкой r. Значения этого множителя также табулированы.

Соответствующие расчетные формулы для аннуитета пренумеран­до можно легко вывести. Так, будущая сто­имость аннуитета пренумерандо может быть найдена по формуле:

.

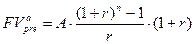Аналогично приведенная стоимость аннуитета пренумерандо может быть найдена по формуле:

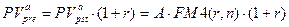
или

.

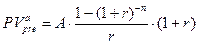Из приведенных формул видно, почему в финансовых таблицах не уточняется, какая схема подразумевается в финансовой сделке — постнумерандо или пренумерандо; содержание финансовой таблицы инвариантно к этому фактору. Однако при применении расчетных формул или финансовых таблиц необходимо строго следить за схемой поступления денежных платежей.