И анизотропия скорости света

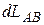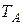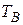Рассмотрим три события, взаимосвязанные световым сигналом и происходящие в пространственных точках A и B элемента твердого тела с физической длиной, равной пространственному расстоянию . Показания часов в точках A и B есть физические времена и . Пусть из точки A через интервал времени 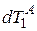отправляется сигнал, который через интервал времени 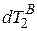прибудет в точку B. Далее сигнал, отраженный от точки B, через интервал времени 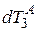прибудет в точку A. События происходят в локальной системе отсчета пространственно-временного континуума. Согласно А. Пуанкаре [1] для стандартной синхронизации часов необходимо определить отношение метрической одновременности события в точке A с событием в точке B, происходящим в середине временного интервала 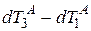. Таким образом, имеем соотношение

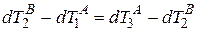, (1.1)

которое дает равенство физических скоростей света 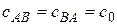вдоль твердого тела. При этом выполняется постулат о равенстве масштабов расстояния, измеряющих длину твердого тела в прямом и обратном направлениях, и используется опытный факт постоянства "средней" скорости света вдоль замкнутого пути, то есть имеем соотношения

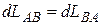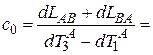
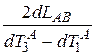, . (1.2)

Однонаправленные скорости света имеют изотропное и инвариантное значение. Согласно Г. Рейхенбаху и А. Грюнбауму [14, 15] события, происходящие во временном интервале 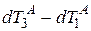есть топологически одновременные события к событию в точке B. Отношение метрической одновременности определяется конвенционально выбором произвольного события из топологически одновременных событий.

Сигнальный метод синхронизации часов, предложенный впервые А. Пуанкаре, дает наблюдаемые интервалы времени в точке A

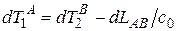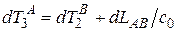, . (1.3)

Различаем несколько случаев. В первом случае интервал собственного времени в точке B определяется выражением

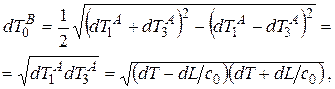(1.4)

где опущены используемые индексы. Запишем квадратичную дифференциальную форму

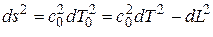, (1.5)

которая представляет собой элемент длины в, так называемой, локальной майкельсоновой системе отсчета пространственно-временного континуума. Форма задана в координатной сетке 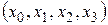с 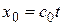. Для риманового многообразия с квадратичной формой

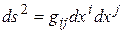(1.6)

и сигнатурой 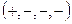имеем

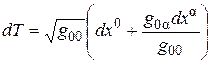, (1.7)

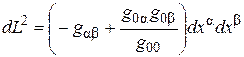, (1.8)

где 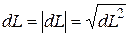и значения индексов 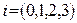, 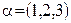. В полугеодезических координатах имеем 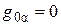, 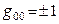. Для определителя справедливо неравенство .

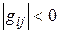Для пространства-времени Минковского в галилеевых координатах получим

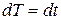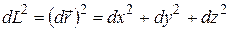, . (1.9)

Здесь интервал физического времени совпадает с интервалом координатного времени и физическая длина есть длина локального радиуса-вектора 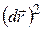с координатами 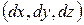. Физические скорости произвольных сигналов равняются координатным. В случае с (1.7) и (1.8) эти равенства не выполняются.

Во втором случае рассмотрим риманово многообразие с квадратичной формой (1.6), имеющей сигнатуру 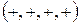. Тогда имеем соотношения

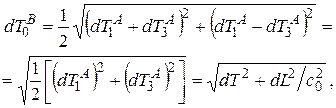(1.10)

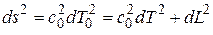, (1.11)

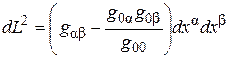(1.12)

и для определителя справедливо неравенство .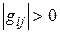

В третьем вырожденном случае положим 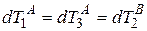и получим

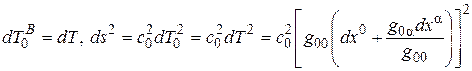. (1.13)

Риманово многообразие с определителем 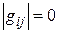имеет сигнатуру с некоторыми нулевыми значениями.

Требует отдельного рассмотрения ещё один невырожденный случай риманова многообразия с сигнатурой .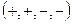

Наиболее общая связь между временными интервалами запишется так

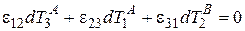, (1.14)

где 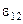, 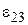и 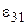есть постоянные элементы антисимметричной временной матрицы перехода между событиями. При стремлении точки 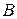к точке 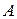интервалы времен 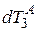и 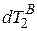приближаются к 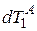, поэтому в пределе получим соотношение

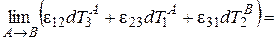
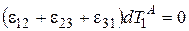. (1.15)

Поскольку 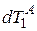есть произвольная величина, то вытекает условие

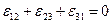, (1.16)

накладываемое на коэффициенты и, следовательно, имеем два независимых параметра.

Из соотношений (1.14) и (1.16) находим следующее равенство

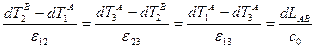, (1.17)

из которого получим значения анизотропных физических и "средней" скорости света

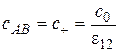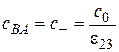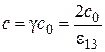, , , (1.18)

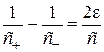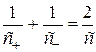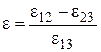, , , (1.19)

где 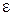есть скалярный параметр временной анизотропии и 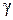- скалярный параметр характеризующий "показатель преломления" для света. Для "средних" скоростей вдоль замкнутого пути должен выполняться следующий предел 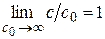. Однонаправленные скорости света неизотропные и неинвариантные значения. Случай с 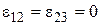соответствует абсолютной одновременности классической физики, в которой сигнальный метод Пуанкаре отсутствует.

Наблюдаемые временные интервалы в точке 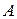равняются

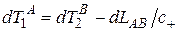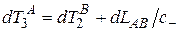, . (1.20)

Значение 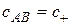определяет скорость света отправленного из точки в точку , а 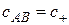- скорость света, отправленного из точки 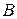в точку 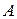твердого тела. Это означает, что в точке 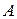не определяется скорость света, отправленного из точки 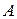в противоположное от точки 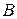напр авление. Аналогично, в точке 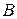не определяется скорость света, отправленного из точки 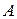в противоположное от точки 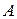направление.

Пр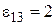и и 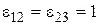из рассматриваемой общей синхронизации часов получим стандартную синхронизацию по Пуанкаре. Преобразования координатной сетки не устраняют физическую анизотропию скорости света. Координатная анизотропия скорости 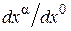в римановом многообразии с (1.6) для изотропных геодезических устраняется преобразованиями координатной сетки, если 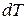есть полный дифференциал. В отличие от работ [16, 17], где приводятся впервые соотношение вида (1.14) для моментов времени, здесь имеем соотношение (1.14) для временных интервалов.