Представление группы преобразований вращения трехмерного псевдоевклидового пространства индекса два

Преобразование Х′=АХ назовем представлением преобразования вращения, если его матрица

A=	a₁₁	a₁₂
a₂₁	a₂₂

комплексна и удовлетворяет условию

A = A=I,

где черточка обозначает операцию

= GA*G,

индекс * – операцию эрмитового сопряжения, а G-метрический тензор

G=	1	0
0	-β	.

причем β = ±1, так что G=G*, G²=I и

= GAG=*	₁₁	-β ₂₁
-β ₁₂	₂₂	.

Очевидно, что

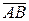=G(AB)*G=G(B*A*)G=(GB*G)(GA*G)= ,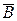

и 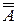= =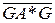G(GА*G)*G=GGAGG=A.

Докажем, что совокупность преобразований вращения обладает групповыми свойствами.

1. Произведение двух преобразований вращения есть преобразование вращения.

Действительно, пусть даны преобразования вращения с матрицами А₁ и А₂; произведение их есть преобразование с матрицей А=А₂А₁. На основании правил перемножения матриц мы можем написать тождество

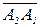А =(А₂А₁)( )=(А₂А₁)(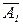 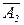)= А₂(А₁ ) .

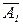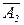Отсюда вследствие равенства A =I имеем:

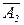A = А₂I =I.

Тем самым требуемое доказано.

2. Преобразование, обратное преобразованию вращения является преобразованием вращения.

Действительно, пусть А-матрица некоторого преобразования вращения иВ= А^-1- матрица преобразования, обратного ему. Из условия A = I следует, что = А^-1. Таким образом В= . Отсюда

В 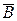= ( 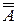)= А= А^-1А=I.

Тем самым требуемое доказано. Таким образом, совокупность преобразований вращения есть группа.

Условие преобразований вращения, записанное в матричной форме, равносильно соотношениям:

А =	а₁₁ ₁₁-β ₁₂а₁₂	а₁₂ ₂₂-β ₂₁а₁₁	=I,
а₂₁ ₁₁-β ₁₂а₂₂	а₂₂ ₂₂-β ₂₁а₂₁

равным I.

Этим условиям можно придать форму отличную от этой формы

А=	₁₁а₁₁-βа₂₁ ₂₁	-β ₂₁а₂₂+а₁₂ ₁₁	=I,
-β ₁₂а₁₁+а₂₁ ₂₂	₂₂а₂₂-βа₁₂ ₁₂

также равной I. Эти системы равенств равносильны.

Любые два из четырех комплексных коэффициентов а_ik определяют все остальные. Более того, они дополнительно связаны соотношением унимодулярности (определитель матрицы А равен ±1), так что два комплексных коэффициента а_ik полностью определяются лишь тремя вещественными параметрами.

Если задан ортонормированный базис е₁, е₂, е₃, то каждый действительный вектор х=х¹е₁+х²е₂+х³е₃ может быть представлен (вообще говоря, комплексной) матрицей размера 2х2

Х=	-βx³	-β(x¹-ix²)	=	x¹Е₁+ x²Е₂+ x³Е₃,
x¹+ix²	βx³

где спиновые матрицы (Паули)

Е₁=	0	-β	,	Е₂=	0	βi	,	Е₃=	-β	0
1	0	i	0	0	β

соответствуют базисным векторам е₁, е₂, е₃. Это соответствие является изоморфизмом, сохраняющим результат сложения векторов и умножения векторов на вещественные числа.

Для каждого вращения вектор вращения х′=х¹′е₁+х²′е₂+х³′е₃ представляется матрицей

Х′=x¹′Е₁+ x²′Е₂+ x³′Е₃=АХ ,

где А – (вообще говоря, комплексная) 2х2 матрица с определителем равным 1:

А=		βb	=	a	-βb
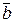
	a	-		,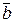

где

a=λ₀-iβλ₃, b=λ₂+i λ₁,

|a|²-β|b|²=λ₀²-β(λ₁²+λ₂²)+λ₃²=1.

А =	\|a\|²-β\|b\|²	0	=I.
0	\|a\|²-β\|b\|²

Комплексные числа a, b определяют соответствующее вращение однозначно, но a, b и -a, -b (а потому матрицы А и -А) описывают одно и тоже вращение. Числа a, b и , 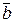называются параметрами (Кэли-Клейна) данного вращения.

Следующие матрицы преобразования описывают правые вращения вокруг положительных координатных осей:

А₁(φ)=	Ch(φ/2)	iβSh(φ/2)
-iSh(φ/2)	Ch(φ/2)

А₂(φ)=	Ch(φ/2)	βSh(φ/2)
Sh(φ/2)	Ch(φ/2)

А₃(φ)=	cos(φ/2)+ iβsin(φ/2)	0	=	е^iβφ/2	0	.
0	cos(φ/2)- iβsin(φ/2)	0	е ^-iβφ/2

Каждая матрица А, описывающая представление вращений в трехмерном псевдоевклидовом пространстве, может быть различными способами представлена в виде произведения трех матриц

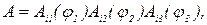
в частности, так:

А=A₃(φ₁)A₂(φ₂)A₃(φ₃)=

=	е^iβ⁽^φ¹⁾^/2	0		Ch(φ2/2)	βSh(φ2/2)		е^iβ(φ3)/2	0	=
0	е^{–iβ(φ1)/2}		Sh(φ2/2)	Ch(φ2/2)		0	е ^{–iβ(φ3)/2}

=	Ch(φ₂/2)е^iβ⁽^φ3+φ1)/2	βSh(φ₂/2)е ^–iβ⁽^φ3-φ¹⁾^/2	.
Sh(φ₂/2)е^iβ⁽^φ3-φ¹⁾^/2	Ch(φ₂/2)е ^–iβ⁽^φ3+φ¹⁾^/2

С другой стороны

А=		βb	=	λ₀+iβλ₃	β(λ₂+i λ₁)	,
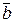
	a	λ₂-i λ₁	λ₀-iβλ₃

так что

λ₀=Ch(φ₂/2)cos((φ₃+φ₁)/2), λ₂= Sh(φ₂/2)cos((φ₃-φ₁)/2),

λ₃=Ch(φ₂/2)sin((φ₃+φ₁)/2), λ₁= -βSh(φ₂/2)sin((φ₃-φ₁)/2),

a= Ch(φ₂/2)exp(-iβ(φ₃+φ₁)/2), b= Sh(φ₂/2)exp(-iβ(φ₃-φ₁)/2).

Четыре параметра (Эйлера) λ₀, λ₁, λ₂, λ₃

λ₀²-βλ₁²-βλ₂²+λ₃²=1

однозначно определяют вращение, причем условие

|a|²-β|b|²=1.

Линейные комбинации матриц I, iЕ₁, iЕ₂ и iЕ₃ с действительными коэффициентами образуют представление четырехмерной алгебры псевдокватернионов, скаляры которой соответствуют действительным кратным матрицы I, а образующие соответствуют матрицам iЕ₁, iЕ₂, iЕ₃, причем

-β(Е₁)²= -β(Е₂)²=(Е₃)²=I,

Е₂Е₃= -Е₃Е₂= -iβЕ₁,Е₃Е₁= -Е₁Е₃= -iβЕ₂,Е₁Е₂= -Е₂Е₁= iЕ₃.

Каждая комплексная матрица размера 2х2 может быть представлена в виде такой линейной комбинации, в частности,

А=λ₀I-i(λ₁Е₁+ λ₂Е₂+ λ₃Е₃),

=λ₀I+i(λ₁Е₁+ λ₂Е₂+ λ₃Е₃).

Снова матрицы А и -А определяют одно и тоже вращение однозначно.

Представление

Х′=x¹′Е₁+ x²′Е₂+ x³′Е₃=АХ

в координатной форме дает:

x¹′=(λ₀λ₀-βλ₁λ₁+βλ₂λ₂-λ₃λ₃)x¹ -2β(λ₁λ₂-λ₃λ₀)x² +2(λ₁λ₃- βλ₂λ₀)x³,

x²′= -2β(λ₂λ₁+λ₃λ₀)x¹+(λ₀λ₀+βλ₁λ₁-βλ₂λ₂-λ₃λ₃)x² +2(λ₂λ₃+βλ₁λ₀)x³,

x³′= -2β(λ₃λ₁+βλ₂λ₀)x¹ -2β(λ₃λ₂-βλ₁λ₀)x²+(λ₀λ₀+βλ₁λ₁+βλ₂λ₂+λ₃λ₃)x³.

Таким образом, задача описания преобразований вращения вполне разрешима. Преобразования вращений в трехмерном псевдоевклидовом пространстве индекса два существенно отличаются от преобразований вращения в трехмерном собственноевклидовом пространстве [1]. Свойства группы псевдоортогональных преобразований также существенно отличаются от свойств группы собственноортогональных преобразований. Геометрии собственноунитарной группы [2] (трехмерной собственноевклидовой геометрии) соответствует представление со значением β= -1. Геометрии псевдоунитарной группы (трехмерной псевдоевклидовой геометрии) соответствует представление со значением β= 1.

<24 25 26 272829 30 >

Дата добавления: 2015-06-01; просмотров: 812;