Типы финслеровых геометрий
Рассмотрим преобразования временного интервала и пространственного расстояния при переходах между движущимися локальными системами 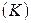 и
и 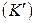 . В системе
. В системе 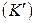 имеем скорости светового сигнала
имеем скорости светового сигнала
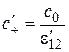 ,
, 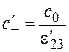 ,
, 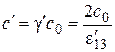 , (2.1)
, (2.1)
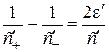 ,
, 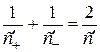 ,
, 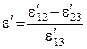 . (2.2)
. (2.2)
Для наглядности примем, что элемент твердого тела расположен вдоль положительного направления 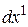
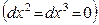 . Он начинает движение от начала координатной сетки системы
. Он начинает движение от начала координатной сетки системы 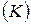 . Физическая длина элемента твердого тела, расположенного вдоль положительного направления
. Физическая длина элемента твердого тела, расположенного вдоль положительного направления 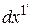 , равняется
, равняется 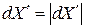 и является, согласно (1.8), абсолютной величиной. Направление
и является, согласно (1.8), абсолютной величиной. Направление 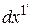 совпадает с направлением
совпадает с направлением 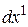 .
.
Рассмотрим первый случай. Воспользуемся методом коэффициента 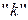 для света идущего от
для света идущего от 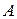 к
к 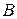 и от
и от 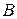 к
к 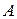 и запишем соотношения
и запишем соотношения
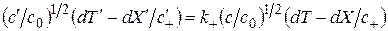 , (2.3)
, (2.3)
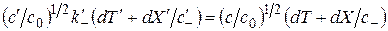 . (2.4)
. (2.4)
В других случаях расположения элемента твердого тела в системах 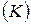 и
и 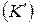 имеют место соотношения, отличные от (2.3) и (2.4) с другими значениями скорости света. Коэффициенты
имеют место соотношения, отличные от (2.3) и (2.4) с другими значениями скорости света. Коэффициенты 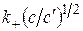 и
и 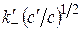 описывают эффект Допплера в прямом и обратном направлениях. Согласно (2.3) и (2.4) получим равенства
описывают эффект Допплера в прямом и обратном направлениях. Согласно (2.3) и (2.4) получим равенства
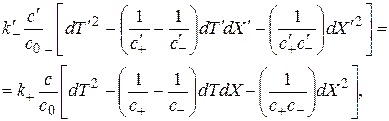 (2.5)
(2.5)
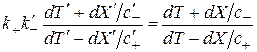 . (2.6)
. (2.6)
При 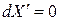 и
и 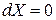 имеем, соответственно,
имеем, соответственно, 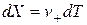 и
и 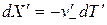 , где
, где 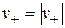 и
и 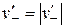 есть относительные скорости систем. Из (2.6) вытекает выражение
есть относительные скорости систем. Из (2.6) вытекает выражение
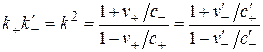 , (2.7)
, (2.7)
из которого находим взаимосвязь между скоростями
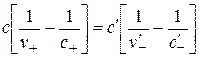 . (2.8)
. (2.8)
При 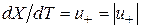 и
и 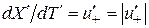 , а также с учетом (2.7), равенство (2.6) для одинаково направленных скоростей преобразуется следующим образом
, а также с учетом (2.7), равенство (2.6) для одинаково направленных скоростей преобразуется следующим образом
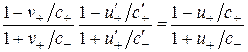 . (2.9)
. (2.9)
Из него, в частности, при 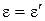 , вытекает закон композиции безразмерных одинаково направленных анизотропных скоростей
, вытекает закон композиции безразмерных одинаково направленных анизотропных скоростей
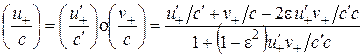 , (2.10)
, (2.10)
множество которых образует абелевую группу.
Определители прямых и обратных преобразований, вытекаемых из соотношений (2.3) и (2.4), равняются 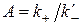 и
и 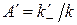
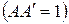 . Учитывая (2.7), получим значения
. Учитывая (2.7), получим значения
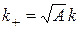 ,
, 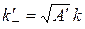 , (2.11)
, (2.11)
где 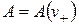 , как и
, как и 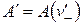 , обладает групповым свойством
, обладает групповым свойством
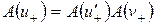 . (2.12)
. (2.12)
Используя закон композиции в виде (2.9) и равенство (2.12), получим уравнение
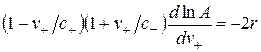 , (2.13)
, (2.13)
имеющее одинаковый вид и для скоростей 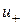 ,
, 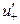 . Инвариантный параметр
. Инвариантный параметр 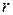 может зависеть от инвариантных значений
может зависеть от инвариантных значений 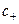 и
и 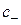 . Интегрируя (2.13) при условии
. Интегрируя (2.13) при условии 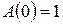 , получим выражение
, получим выражение 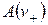 , преобразования и квадрат форм-инвариантной метрической функции в следующих типах локальных финслеровых геометрий.
, преобразования и квадрат форм-инвариантной метрической функции в следующих типах локальных финслеровых геометрий.
Тип I 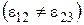 .
.
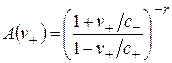 , (2.14)
, (2.14)
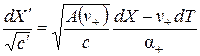 ,
, 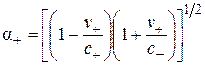 , (2.15)
, (2.15)
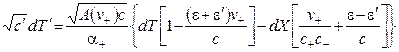 , (2.16)
, (2.16)
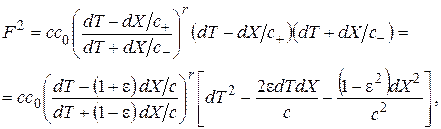 (2.17)
(2.17)
Тип II 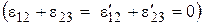 .
.
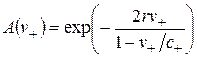 , (2.18)
, (2.18)
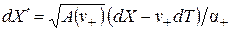 ,
, 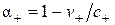 , (2.19)
, (2.19)
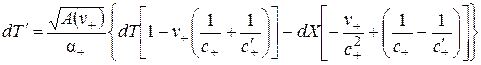 , (2.20)
, (2.20)
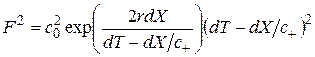 , (2.21)
, (2.21)
Значение 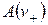 и преобразования в типе II вытекают из формул (2.13), (2.15)-(2.17) в типе I формально при
и преобразования в типе II вытекают из формул (2.13), (2.15)-(2.17) в типе I формально при 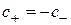 .
.
Тип III 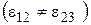 .
.
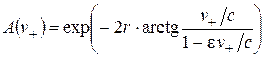 , (2.22)
, (2.22)
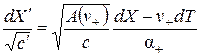 ,
, 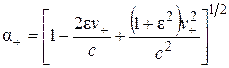 , (2.23)
, (2.23)
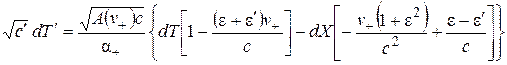 , (2.24)
, (2.24)
 . (2.25)
. (2.25)
Тип IV 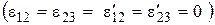 .
.
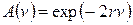 , (2.26)
, (2.26)
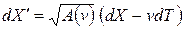 ,
, 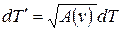 , (2.27)
, (2.27)
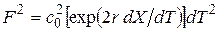 . (2.28)
. (2.28)
Формулы для типа III получены на основании результатов работы [18]. Формулы для типа IV получены из соотношений (2.18)-(2.21) в типе II при 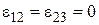 . При
. При 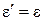 и
и 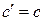 первые три типа соответствуют для определенных значений
первые три типа соответствуют для определенных значений 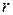 и
и 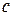 трём типам локальных финслеровых геометрий с индикатрисой постоянной кривизны, рассмотренных в работе [19].
трём типам локальных финслеровых геометрий с индикатрисой постоянной кривизны, рассмотренных в работе [19].
Рассмотрим случай с 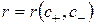 и запишем интервал собственного времени в типе I так
и запишем интервал собственного времени в типе I так
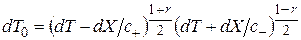 . (2.29)
. (2.29)
Равенство 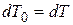 соответствует геометрии Галилея и имеет место при
соответствует геометрии Галилея и имеет место при 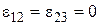 , если выполняются соотношения
, если выполняются соотношения
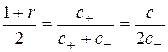 ,
, 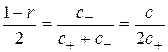 . (2.30)
. (2.30)
Из (2.30) получим инвариантное значение параметра
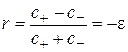 (2.31)
(2.31)
и, следовательно, интервал собственного времени примет вид
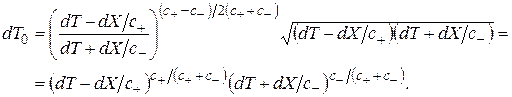 (2.32)
(2.32)
Квадрат финслеровой метрической функции запишется так
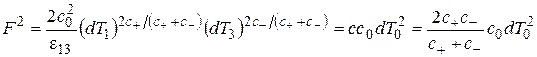 .(2.33)
.(2.33)
В работах [13], [19] и [20] рассматривается анизотропия физической скорости света ( 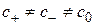 ,
, 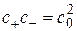 ,
,  ) для квадрата финслеровой метрической функции (2.33) без коэффициента
) для квадрата финслеровой метрической функции (2.33) без коэффициента 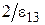 . Там же приводятся соответствующие нелинейные и линейные преобразования для случая двумерного и четырехмерного финслерового пространства-времени с одним скалярным параметром. Случай анизотропии координатной скорости света с
. Там же приводятся соответствующие нелинейные и линейные преобразования для случая двумерного и четырехмерного финслерового пространства-времени с одним скалярным параметром. Случай анизотропии координатной скорости света с  исследуется в [21].
исследуется в [21].
Для случая 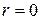 в типе I имеем
в типе I имеем
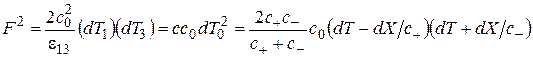 .(2.34)
.(2.34)
В случае 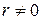 и
и 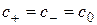 получим
получим
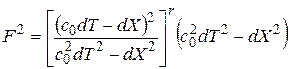 . (2.35)
. (2.35)
Обобщением выражения (2.35) с учетом (1.6)-(1.8) для четырехмерного пространства-времени является
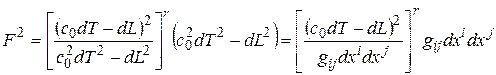 . (2.36)
. (2.36)
В отличие от работы [22] в (2.36) отсутствует четырехмерный вектор 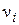 с
с 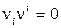 , указывающей локально выделенные направления. Обобщение результатов работы [22] на случай анизотропии координатной скорости света дается в [32]. Следует отметить, что добавление к рассмотренным преобразованиям ещё двух
, указывающей локально выделенные направления. Обобщение результатов работы [22] на случай анизотропии координатной скорости света дается в [32]. Следует отметить, что добавление к рассмотренным преобразованиям ещё двух 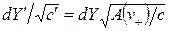 и
и 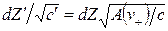 не приводят к замене
не приводят к замене 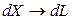 в приведенных метрических функциях.
в приведенных метрических функциях.
В галилеевых координатах имеем квадрат финслеровой метрической функции
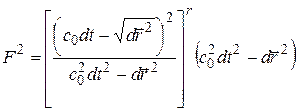 , (2.37)
, (2.37)
требующей отдельного рассмотрения.
Дата добавления: 2015-06-01; просмотров: 778;
