Пространстве индекса два
Линейное преобразование х′=Ахс вещественной матрицей
| a11 | a12 | a13 | ||
| A= | a21 | a22 | a23 | |
| a31 | a32 | a33 |
назовем преобразованием вращения, если его матрица удовлетворяет условию
A  =
=  A=I,
A=I,
где черточка обозначает операцию
 = GAТG,
= GAТG,
индекс T – операцию транспонирования, G – метрический тензор,
| -α | 0 | 0 | ||
| G= | 0 | -β | 0 | |
| 0 | 0 | αβ | , |
причем a,β=±1, так что G=GT, G2=I и
| a11 | αβa21 | -βa31 | ||
 =GATG= =GATG=
| αβa12 | a22 | -αa32 | |
| -βa13 | -αa23 | a33 | . |
Очевидно, что
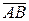 =G(AB)TG=G(BTAT)G=(GBTG)(GATG)=
=G(AB)TG=G(BTAT)G=(GBTG)(GATG)= 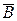
 ,
,
и 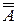 =
= 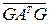 =G(GАТG)TG=GGAGG=A.
=G(GАТG)TG=GGAGG=A.
Преобразование вращения в трехмерном псевдоевклидовом векторном пространстве сохраняет квадраты модулей векторов. Такое преобразование является собственным вращением, если оно сохраняет также векторное произведение двух векторов и det ||A||=1. Преобразование с det ||A||= -1 является несобственным вращением или вращением с отражением.
Пусть е1, е2, е3 – любой ортонормированный базис, и пусть
х=х1е1+х2е2+х3е3 и х′=х1′е1+х2′е2+х3′е3.
Каждое преобразование вращения задается формулами
х1′= a11 х1+a12 х2 +a13х3,
х2′= a21 х1+a22 х2+a23х3,
х3′= a31 х1+a32 х2+a33х3
или в матричной форме
Х′= AХ,
где для собственных вращений det(A)=1.
Так как рассматриваемая система координат является ортонормированной, действительная матрица А, описывающая каждое вращение, определяется системой равенств
| а11а11+αβа12а12-βа13а13 | αβа11а21+а12а22-αа13а23 | -βа11а31-αа12а32+ а13а33 | ||
А  = =
| а21а11+αβа22а12-βа23а13 | αβа21а21+а22а22-αа23а23 | -βа21а31-αа22а32+ а23а33 | =I |
| а31а11+αβа32а12-βа33а13 | αβа31а21+а32а22-αа33а23 | -βа31а31-αа32а32+ а33а33 |
или, что равносильно,
| а11а11+αβа21а21-βа31а31 | а11а12+αβа21а22-βа31а32 | а11а13+αβа21а23- βа31а33 | ||
 А= А=
| αβа12а11+ а22а21-αа32а31 | αβа12а12+ а22а22-αа32а32 | αβа12а13+ а22а23- αа32а33 | =I. |
| -βа13а11- αа23а21+ а33а31 | -βа13а12- αа23а22+ а33а32 | -βа13а13- αа23а23+ а33а33 |
Любые три из коэффициентов аik определяют все остальные. Геометрически коэффициент аik определяет угол между базисным вектором ei и повернутым базисным вектором
ek′=Aek= 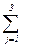 аjkej,
аjkej,
аik=(ei ek′).
Преобразование вращения поворачивает радиус – вектор х каждой точки трехмерного псевдоевклидового пространства на угол поворота δ вокруг направленной оси вращения, точки которой инвариантны. Угол поворота δ, а также направляющие углы положительной оси вращения определяются формулами
Chδ=  (Tr (A)-1)=
(Tr (A)-1)=  (a11+ a22+ a33-1)=2λ02-1
(a11+ a22+ a33-1)=2λ02-1
αа23+ а32=2с1Shδ=4λ1λ0,
-а31-βа13=2с2Shδ=4λ2λ0,
βа12-αа21=2с3Shδ=4λ3λ0.
Либо знак угла δ, либо направление оси вращения могут выбираться произвольно.
Матрица преобразования А, соответствующая данному вращению, описываемая числами δ, с1, с2,…, с7, есть
| -αс1с1 | -βс1с2 | αβс1с3 | ||
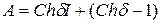
| -αс2с1 | -βс2с2 | αβс2с3 | + |
| -αс3с1 | -βс3с2 | αβс3с3 |
| 0 | βс3 | -βс2 | ||
| +Shδ | -αс3 | 0 | αс1 | . |
| -с2 | с1 | 0 |
Четыре симметричных параметра (Эйлера)
λ0  , λ1
, λ1 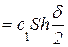 , λ2
, λ2 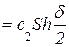 , λ3
, λ3 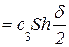 ,
,
λ02-αλ12-βλ22+αβλ32=1
-αс12-βс22+αβс32= -1
однозначно определяют вращение, так как из выражения для матрицы А следует:
| -α(λ1λ1- αλ0λ0) | -β(λ1λ2- λ3λ0) | αβ(λ1λ3- αλ2λ0) | ||
| А= -I+2* | -α(λ2λ1+ λ3λ0) | -β(λ2λ2- βλ0λ0) | αβ(λ2λ3+ βλ1λ0) | . |
| -α(λ3λ1+αλ2λ0) | -β(λ3λ2- βλ1λ0) | αβ(λ3λ3+αβλ0λ0) |
При этом
| -α(λ1λ1- αλ0λ0) | -β(λ1λ2+ λ3λ0) | αβ(λ1λ3+ αλ2λ0) | ||
 = -I+2* = -I+2*
| -α(λ2λ1- λ3λ0) | -β(λ2λ2- βλ0λ0) | αβ(λ2λ3- βλ1λ0) | . |
| -α(λ3λ1- αλ2λ0) | -β(λ3λ2+βλ1λ0) | αβ(λ3λ3+αβλ0λ0) |
Будем считать для определенности α=β=1. В принятом предположении
Chδ=  (Tr (A)-1)=
(Tr (A)-1)=  (a11+ a22+ a33-1)=2λ02-1
(a11+ a22+ a33-1)=2λ02-1
βа23+ а32=2с1Shδ=4λ1λ0,
-а31-βа13=2с2Shδ=4λ2λ0,
βа12-βа21=2с3Shδ=4λ3λ0.
| -βс1с1 | -βс1с2 | с1с3 | 0 | βс3 | -βс2 | |||
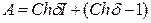
| -βс2с1 | -βс2с2 | с2с3 | +Shδ | -βс3 | 0 | βс1 | . |
| -βс3с1 | -βс3с2 | с3с3 | -с2 | с1 | 0 |
Четыре симмметричных параметра (Эйлера)
λ02-λ12-βλ22+λ32=1,
-βс12-βс22+с32 = -1,
однозначно определяют вращение, так как из выражения для матрицы А следует:
| -β(λ1λ1- βλ0λ0) | -β(λ1λ2- λ3λ0) | λ1λ3 -βλ2λ0 | ||

| -β(λ2λ1+ λ3λ0) | -β(λ2λ2-βλ0λ0) | λ2λ3+βλ1λ0 | |
| -β(λ3λ1+βλ2λ0) | -β(λ3λ2-βλ1λ0) | λ3λ3+ λ0λ0 | , |
при этом
| -β(λ1λ1- βλ0λ0) | -β(λ1λ2+ λ3λ0) | λ1λ3+βλ2λ0 | ||
 = -I+2* = -I+2*
| -β(λ2λ - λ3λ0) | -β(λ2λ2- βλ0λ0) | λ2λ3- βλ1λ0 | |
| -β(λ3λ1-βλ2λ0) | -β(λ3λ2+βλ1λ0) | λ3λ3+ λ0λ0 | , |
а параметры λ0, λ1, λ2, λ3 и–λ0, –λ1, –λ2, – λ3 представляют одно и то же вращение.
Следующие матрицы преобразования описывают правые вращения вокруг положительных координатных осей:
| 1 | 0 | 0 | |
| А1(φ)= | 0 | Chφ | βShφ |
| 0 | Shφ | Chφ |
| Chφ | 0 | -βShφ | |
| А2(φ)= | 0 | 1 | 0 |
| -Shφ | 0 | Chφ |
| cosφ | βsinφ | 0 | ||
| А3(φ)= | -βsinφ | cosφ | 0 | |
| 0 | 0 | 1 | . |
Заметим, что
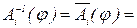 Аi(-φ), i= 1, 2, 3.
Аi(-φ), i= 1, 2, 3.
Каждая матрица А, описывающая собственное вращение в трехмерном псевдоевклидовом пространстве, может быть различными способами представлена в виде произведения трех матриц
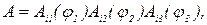
в частности, так:
А=A3(φ1)A2(φ2)A3(φ3)=
| cosφ1 | βsinφ1 | 0 | Chφ2 | 0 | -βShφ2 | cosφ3 | βsinφ3 | 0 | ||||
| = | -βsinφ1 | cosφ1 | 0 | * | 0 | 1 | 0 | * | -βsinφ3 | cosφ3 | 0 | = |
| 0 | 0 | 1 | -Shφ2 | 0 | Chφ2 | 0 | 0 | 1 |
| cosφ1Chφ2cosφ3 - sinφ1sinφ3 | βcosφ1Chφ2sinφ3+βsinφ1cosφ3 | -βcosφ1Shφ2 | ||
| = | -βsinφ1Chφ2cosφ3-βcosφ1sinφ3 | -sinφ1Chφ2sinφ3+ cosφ1cosφ3 | sinφ1Shφ2 | . |
| -Shφ2cosφ3 | -βShφ2sinφ3 | Chφ2 |
Три угла (Эйлера) φ1, φ2, φ3,однозначно определяют вращение; в свою очередь они однозначно определяются данным вращением за исключением случая, когда φ2=0 (карданов подвес).
Обратное вращение А-1=  (переводящее вектор х′ в исходный вектор х) представляется матрицей
(переводящее вектор х′ в исходный вектор х) представляется матрицей
 =A3(-φ3)A2(-φ2)A3(-φ1)=
=A3(-φ3)A2(-φ2)A3(-φ1)=
| cosφ1Chφ2cosφ3- sinφ1sinφ3 | -βsinφ1Chφ2cosφ3-βcosφ1sinφ3 | βShφ2cosφ3 | ||
| = | βcosφ1Chφ2sinφ3+βsinφ1cosφ3 | -sinφ1Chφ2sinφ3+ cosφ1cosφ3 | Shφ2sinφ3 | …. |
| cosφ1Shφ2 | -βsinφ1Shφ2 | Chφ2 |
Существуют шесть способов, которыми матрицу вращения можно выразить путем вращения вокруг двух различных осей координат. Кроме того, существует шесть способов представления матриц вращения в виде произведения вращений вокруг трех различных осей координат, в частности, так:
| 1 | 0 | 0 | Chφ2 | 0 | -βShφ2 | cosφ3 | βsinφ3 | 0 | ||||
| A=A1(φ1) A2(φ2) A3(φ3)= | 0 | Chφ1 | βShφ1 | 0 | 1 | 0 | -βsinφ3 | cosφ3 | 0 | = | ||
| 0 | Shφ1 | Chφ1 | -Shφ2 | 0 | Chφ2 | 0 | 0 | 1 |
| Chφ2cosφ3 | -βChφ2sinφ3 | -βShφ2 | ||
| = | -βShφ1Shφ2cosφ3-βChφ1sinφ3 | -Shφ1Shφ2sinφ3+Chφ1cosφ3 | βShφ1Chφ2 | |
| -Chφ1Shφ2cosφ3-βShφ1sinφ3 | -βChφ1Shφ2sinφ3+Shφ1cosφ3 | Chφ1Chφ2 |
при  =A3(-φ3) A2(-φ2) A1(-φ1)=
=A3(-φ3) A2(-φ2) A1(-φ1)=
| Chφ2cosφ3 | -βShφ1Shφ2cosφ3-βChφ1sinφ3 | βChφ1Shφ2cosφ3+ Shφ1sinφ3 | ||
| = | -βChφ2sinφ3 | -Shφ1Shφ2sinφ3+ Chφ1cosφ3 | Chφ1Shφ2sinφ3-βShφ1cosφ3 | . |
| Shφ2 | -Shφ1Chφ2 | Chφ1Chφ2 |
Дата добавления: 2015-06-01; просмотров: 683;
