Замкнутых дискретных систем

Замкнутая линейная амплитудная импульсная система (АИС), включающая в себя импульсный элемент (ИЭ), непрерывную часть (НЧ) и датчик рассогласования (ДР), может быть представлена в виде структурной схемы [15], изображенной на рис. 1.10. Она состоит из простейшего импульсного элемента (ПИЭ) с периодом дискретности T, формирующего элемента (ФЭ) с передаточной функцией W_ФЭ(s) и непрерывной части (НЧ), разделенной на два участка с передаточными функциями W₁(s) и W₂(s).

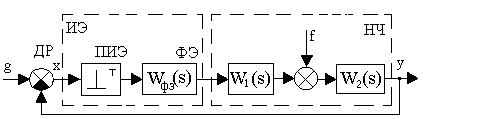
Рис. 1.10. Структурная схема замкнутой импульсной системы

Для получения математического описания замкнутой импульсной системы установим связи между выходной управляемой величиной y и рассогласованием x с одной стороны и задающим g и возмущающим f воздействиями с другой стороны.

Определим сначала дискретную передаточную функцию замкнутой импульсной системы по задающему воздействию, для чего примем f(t)=0.

Ко входу простейшего импульсного элемента прикладывается рассогласование, определяемое как

x(t) = g(t) - y(t).

Так как простейший импульсный элемент замыкается лишь в дискретные моменты времени t = nT, то на его выходе образуется сигнал, который можно записать через решетчатые функции в виде

x[n] = g[n] - y[n]. (1.65)

Подвергнув уравнение (1.65) z-преобразованию, получим уравнение ошибки в изображениях:

X(z) = G(z) - Y(z). (1.66)

Уравнение разомкнутой импульсной системы

Y(z,s) = W(z,s) X(z), (1.67)

где

W(z,s) = Z_s{W_ФЭ(s)W₁(s)W₂(s)}.

При s = 0 получим изображение решетчатой функции y[n]

Y(z) = W(z) X(z). (1.68)

Подставив (1.68) в уравнение замыкания (1.66), найдем уравнение замкнутой импульсной системы относительно изображения рассогласования:

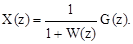(1.69)

Если далее подставить (1.69) в (1.67), то получим уравнение замкнутой импульсной системы, описывающее процессы в любой момент времени t = (n+s)T:

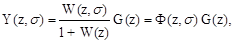(1.70)

где

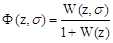. (1.71)

Функция Ф(z,s) называется дискретной передаточной функцией замкнутой импульсной системы и равняется отношению модифицированного z-изображения выходной управляемой величины замкнутой импульсной системы к z-изображению входного задающего воздействия при нулевых начальных условиях:

.

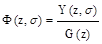Дискретная передаточная функция замкнутой импульсной системы, также как и разомкнутой, зависит от относительного времени s.

При s = 0, то есть для моментов времени t = nT

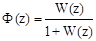. (1.72)

Уравнение ошибки в изображениях для любого момента времени t = (n+s)T, характеризующее воспроизведение системой задающего воздействия, имеет вид

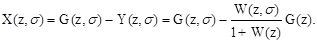(1.73)

Из последнего выражения следует, что для любого s (любого момента времени) передаточную функцию замкнутой импульсной системы по ошибке относительно задающего воздействия определить невозможно, так как она зависела бы от входного сигнала g.

Однако, дискретная передаточная функция замкнутой импульсной системы по ошибке относительно задающего воздействия существует при s = 0, т.е. для моментов времени t = nT:

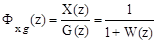. (1.74)

Далее найдем изображение выходной управляемой величины от возмущающего воздействия f(t) при g(t) = 0, для чего исходную структурную схему системы (рис. 1.10) преобразуем к виду, показанному на рис. 1.11.

На основании приведенной структурной схемы z-преобразование выходной величины системы можно записать в следующем виде

Y(z,s) = X₁(z,s) - X₂(z,s) = Z_s{W₂(s) F(s)} - W(z,s) Y(z). (1.75)

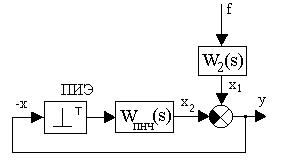
Рис. 1.11. Приведенная структурная схема замкнутой

импульсной системы

При s = 0, т.е. для дискретных моментов времени t = nT, это уравнение можно переписать как

.

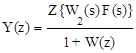Подставив его в (1.75), получим уравнение для выходной величины системы в z-изображениях для любого момента времени t = (n+s)T:

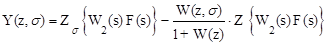. (1.76)

Отсюда следует, что ввести понятие дискретной передаточной функции замкнутой импульсной системы по возмущающему воздействию невозможно, так как она зависела бы от последнего. Для дискретных моментов времени t = nT, то есть при s = 0, можно написать лишь следующее отношение

,

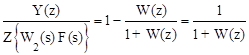которое совпадает с выражением для дискретной передаточной функции замкнутой импульсной системы по ошибке относительно задающего воздействия в дискретные моменты времени t = nT.

Таким образом, в отличие от непрерывных систем, для дискретных систем при любых значениях s имеет место только одна передаточная функция, а для s = 0 - две передаточные функции относительно задающего воздействия; передаточные функции по возмущающему воздействию не существуют.