Передаточные функции разомкнутых импульсных систем
Разомкнутая линейная амплитудная импульсная система (АИС) может быть схематически представлена в виде последовательного соединения импульсного элемента (ИЭ) и непрерывной части (НЧ) (рис. 1.6). Подобные системы называют импульсными фильтрами.
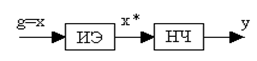
Рис. 1.6. Функциональная схема разомкнутой импульсной системы:
ИЭ - импульсный элемент; НЧ - непрерывная часть
Импульсный элемент преобразует задающее воздействие g(t) в последовательность импульсов x*, амплитуда которых пропорциональна входному непрерывному сигналу. Импульсная последовательность после прохождения через непрерывную часть вследствие сглаживающих свойств последней превращается в непрерывную величину на выходе y(t).
При исследовании импульсной системы ее структуру приводят к расчетной схеме (рис. 1.7) путем замены импульсного элемента последовательным соединением простейшего импульсного элемента (ПИЭ) и непрерывного фильтра, который называется формирующим элементом (ФЭ). Простейший импульсный элемент преобразует непрерывный сигнал в мгновенные импульсы в виде d-функций, модулированные по площади, а формирующий элемент формирует импульс заданной формы из d-функций, соответствующей форме выходного импульса реального импульсного элемента. Форма импульса реального импульсного элемента определяет импульсную функцию формирующего элемента wФЭ(t). Следовательно, передаточная функция формирующего элемента может быть определена как изображение формы импульса по Лапласу, т.е.
WФЭ(s)=L[wФЭ(t)]. (1.52)
Формирующий элемент объединяется с непрерывной частью системы в приведенную непрерывную часть.
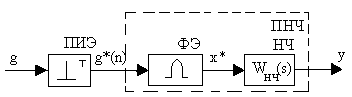
Рис. 1.7. Расчетная функциональная схема разомкнутой импульсной системы: ПИЭ - простейший импульсный элемент; ФЭ - формирующий элемент; НЧ - непрерывная часть; ПНЧ - приведенная непрерывная часть
Таким образом, линейную импульсную систему с амплитудно-импульсной модуляцией приводят к расчетной структуре, состоящей из последовательного соединения простейшего импульсного элемента и приведенной непрерывной части, передаточная функция которой
WПНЧ(s) = WФЭ(s)´WНЧ(s), (1.53)
где WНЧ(s) - передаточная функция непрерывной части системы.
Для получения математического описания разомкнутой импульсной системы установим связь между ее входной и выходной координатами.
Если внешнее воздействие g(t) приложено ко входу простейшего импульсного элемента, то на его выходе появляется последовательность мгновенных импульсов g*[nT], модулированных внешним воздействием (рис. 1.8). Выходной сигнал простейшего импульсного элемента
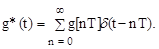 (1.54)
(1.54)
Таким образом, на выходе простейшего импульсного элемента образуются мгновенные импульсы (d-функции), площадь каждого из которых пропорциональна значениям входной величины в дискретные моменты времени. На рис. 1.8 d-функции условно изображены в виде стрелок, длина которых соответствует дискретным значениям входной величины.
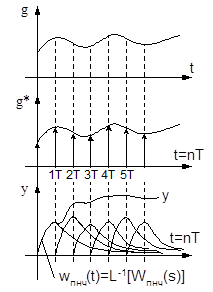
Рис. 1.8. Временные диаграммы изменения сигналов
импульсной разомкнутой системы
Последовательность импульсов g* воздействует на приведенную непрерывную часть системы. Реакция приведенной непрерывной части на мгновенный импульс представляет собой ее импульсную функцию
wпнч(t) = L-1[WПНЧ(s)], (1.55)
где L-1 - знак обратного преобразования Лапласа.
На основании принципа суперпозиции можно определить выходную величину разомкнутой линейной импульсной системы
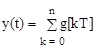 wпнч(t-kT) . (1.56)
wпнч(t-kT) . (1.56)
Очевидно, что непрерывно меняющаяся выходная величина разомкнутой импульсной системы определяется мгновеными значениями входного воздействия в дискретные моменты времени t = nT.
Для дискретных моментов времени
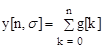 wпнч[n-k,s] . (1.57)
wпнч[n-k,s] . (1.57)
Последнее выражение устанавливает связь между входной g и выходной y величинами разомкнутой импульсной системы, которые представлены решетчатыми функциями.
Подвергнув формулу (1.57) z-преобразованию, на основании свертки функций получим уравнение разомкнутой импульсной системы в изображениях:
Y(z,s) = W(z,s)G(z), (1.58)
где Y(n,s)=Zs{y[n,s]}; G(z)=Z{g[n]}; W(z,s)=Zs{wпнч[n,s]}.
Выражение
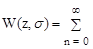 wпнч[n,s]z-n (1.59)
wпнч[n,s]z-n (1.59)
называется дискретной передаточной функцией разомкнутой импульсной системы .
Особенностью дискретной передаточной функции, как следует из (1.59), является то, что она зависит от относительного времени s, т.е. изменяется с течением времени внутри каждого периода дискретности.
Однако большинство задач по исследованию дискретных систем может быть решено при использовании передаточной функции W(z).
При практических расчетах часто представляют z-преобразование непрерывной функции wпнч(t) в виде выражения
W(z,s)=Zs{WПНЧ(s)}. (1.60)
Таким образом, дискретная передаточная функция определяется по импульсной функции приведенной непрерывной части системы. В случае, когда приведенная непрерывная часть состоит из параллельно включенных звеньев и ее передаточная функция
WПНЧ(s) = 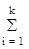 Wi(s),
Wi(s),
дискретная передаточная функция может быть определена суммированием передаточных функции, определенных для каждого звена в отдельности:
W(z) = 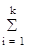 Wi(z).
Wi(z).
В отличие от непрерывных систем подобное правило не имеет места для случая последовательно включенных звеньев с общей передаточной функцией
WПНЧ(s) = 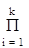 Wi(s)
Wi(s)
и общим импульсным элементом на входе. В этом случае
W(z) ¹ 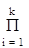 Wi(z)
Wi(z)
и передаточная функция W(z) должна определяться по результирующей импульсной функции приведенной непрерывной части системы.
Для нахождения дискретных передаточных функций можно пользоваться таблицами соответствий между функциями времени, их изображениями по Лапласу и их z-изображениями.
В большинстве случаев импульсный элемент формирует прямоугольные или близкие к прямоугольным импульсы длительности Tимп = gТ , то есть импульсная функция формирующего элемента имеет вид, представленный на рис. 1.9,а [15].
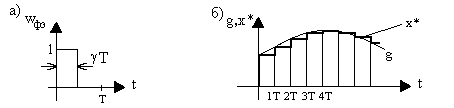 Рис. 1.9. Выходная величина формирующего элемента
Рис. 1.9. Выходная величина формирующего элемента
Прямоугольный импульс единичной высоты и длительности gT можно представить как
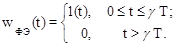
В этом случае передаточная функция формирующего элемента
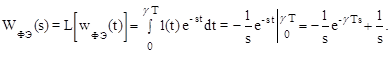
Отсюда
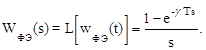 (1.61)
(1.61)
Тогда расчетное соотношение для дискретной передаточной функции разомкнутой импульсной системы можно получить из (1.60)
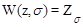 {
{ 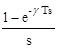 Wнч(s) }= W1(z,s) - W1g(z,s), (1.62)
Wнч(s) }= W1(z,s) - W1g(z,s), (1.62)
где
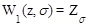 {
{ 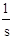 Wнч(s) };
Wнч(s) };
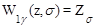 {
{ 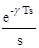 Wнч(s) }.
Wнч(s) }.
Передаточную функцию W1g(z,s) можно выразить через передаточную функцию W1(z,s) в соответствии с теоремой сдвига (1.32). В результате получим
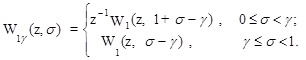
При s = 0 W1g(z) = z-1 W1(z,1-g).
Частные случаи.
1. Если импульсный элемент генерирует короткие по сравнению с периодом дискретности прямоугольные импульсы, т.е. g << 1, то можно приближенно принять е- gТs »1 - gTs. Тогда получим
W(z,s) = gT Zs{WНЧ(s)}. (1.63)
Формула (1.63) справедлива, если пренебречь влиянием конечной длительности импульса. В большинстве случаев для выполнения достаточно, чтобы постоянные времени непрерывной части системы были больше длительности импульса, т.е. T i >> gТ (i = 1, 2, 3, ...).
2. Если импульсный элемент генерирует прямоугольные импульсы, длительность которых совпадает с периодом дискретности, т.е. g = 1 (рис. 1.9,б). Подобным образом работают, например, системы с ЦВМ. Такой формирующий элемент называется экстраполятором нулевого порядка или запоминающим элементом. Дискретная передаточная функция в этом случае будет
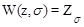 {
{ 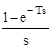 Wнч(s)}=
Wнч(s)}= 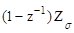 {
{ 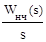 }.
}.
Таким образом, расчетное соотношение для дискретной передаточной функции разомкнутой цифровой системы упрощается:
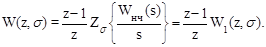 (1.64)
(1.64)
Пример. Определить дискретную передаточную функцию импульсной системы, у которой импульсный элемент формирует прямоугольные импульсы длительности g = 0,2 с периодом дискретности T=1 c, а непрерывная часть задана передаточной функцией:
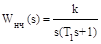 при k=10 c-1 , T1=2 c.
при k=10 c-1 , T1=2 c.
Р е ш е н и е . Дискретную передаточную функцию разомкнутой импульсной системы находим по выражению (1.62), представляя дробь Wнч(s)/s в виде суммы элементарных дробей:
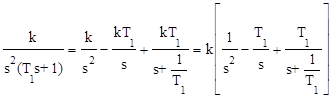 .
.
С помощью таблицы соответствий найдем модифицированное z-преобразование для каждого из слагаемых в правой части полученного выражения:
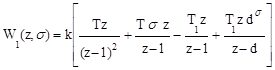 ,
,
где 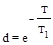 .
.
Частные случаи.
1. При s = 0
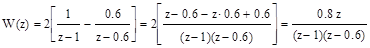 .
.
2. При s = 0 и g =1
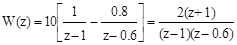 .
.
3. При s = 0 и g << 1, так как T1 >> gТ
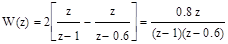 .
.
Дата добавления: 2015-06-01; просмотров: 2465;
