Математический аппарат исследования дискретных систем

Величины, описывающие поведение автоматических систем, представляют собой функции времени. Математическое исследование дискретных систем существенно упрощается в том случае, когда все величины рассматриваются в дискретные равноотстоящие моменты времени.

Решетчатые функции и разностные уравнения.Решетчатая функция времени x[nT], или в сокращенной записи x[n] - это математическая функция, значения которой определены в дискретные равноотстоящие друг от друга моменты времени t = nT, где n - целое положительное число 0, 1, 2 ..., а Т - период дискретности. То есть решетчатая функция представляет собой числовую последовательность:

x[0], x[1T], x[2T], x[3T], ... , x[kT], ... .

Если период дискретности T задан, то решетчатая функция однозначно формируется из исходной непрерывной. Операция замены непрерывной функции решетчатой

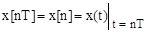(1.2)

показана на рис. 1.3.

Обратная задача - формирование непрерывной функции из решетчатой - не может быть решена однозначно без дополнительных сведений о поведении функции в интервале между точками t = nT, так как функции, заданной в дискретные моменты времени, может соответствовать бесконечное множество непрерывных функций.

Возникает вопрос, при каких условиях возможно точное восстановление квантованной функции. Ответ на него дает теорема Котельникова-Шеннона [5]: непрерывный сигнал x(t), частотный спектр которого ограничен полосой 0 < f < f_п, полностью определяется последовательностью своих дискретных значений, если период повторения Т этих значений удовлетворяет условию

Т < 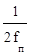или Т < 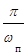, (1.3)

где f_п[Гц], w_п [с^-1] - частота пропускания.

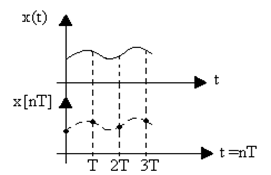
Рис. 1.3.Временные диаграммы изменения непрерывной функции x(t)

и решетчатой функции x[nT]

Смещенная решетчатая функция времени представляет собой числовую последовательность:

x[sT], x[1T+sT], x[2T+sT], x[3T+sT], ... , x[kT+sT], ... ,

образованную в результате выборки значений функции x(t) в точках t = nT+sT оси времени

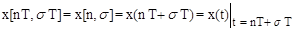, (1.4)

где s - постоянное число из интервала 0 £ s < 1.

Параметр s рассматривается в качестве относительного (безразмерного) времени, отсчитываемого от начала очередного (n-го) интервала повторения. Его иногда называют локальным (местным) временем.

Смещенная решетчатая функция x[n,s] для всех возможных значений s позволяет однозначно восстановить “породившую” ее непрерывную функцию x(t).

Своего рода “дискретными аналогами” производных и интегралов непрерывных функций для решетчатых функций являются конечные разности и суммы.

Конечные разности решетчатых функций бывают двух видов: прямые (упреждающие) и обратные (отстающие).

Первая прямая разность

Dx[n,s]=x[n+1,s]-x[n,s] (1.5)

и первая обратная разность

Ñx[n,s]=x[n,s]-x[n-1,s]. (1.6)

Разности произвольного порядка k определяются при помощи рекуррентных соотношений:

D^k x[n,s] = D{D^k-1 x[n,s]}= D^k-1 x[n+1,s] - D^k-1 x[n,s], (1.7)

Ñ^k x[n,s] = Ñ{Ñ^k-1 x[n,s]}= Ñ^k-1 x[n,s] - Ñ^k-1 x[n-1,s] (1.8)

или формул общего вида

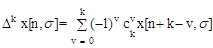, (1.9)

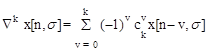, (1.10)

где биноминальные коэффициенты (число сочетаний)

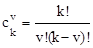. (1.11)

Прямая и обратная разности связаны соотношением

Ñ^k x[n,s] = D^k x[n-k,s]. (1.12)

Соотношения (1.9) и (1.10) показывают, что для вычисления разности k-го порядка в некоторой точке [n,s] требуется знать значение функции x[n,s] в (k+1)-й точке. Для прямой разности этими значениями являются текущее x[n,s] и последующие x[n+1,s], x[n+2,s], ..., x[n+k,s] значения; вычисление обратной разности требует знания предыдущих x[n-1,s], x[n-2,s], ..., x[n-k,s] значений последовательности x[n,s].

Обратные разности обладают важной особенностью. Если решетчатая функция определена только для положительных значений аргумента, т.е. x[n,s] º 0 при n < 0, то, как следует из (1.10), в точке n = 0 k-я разность

Ñ^k x[0,s] = x[0,s] (1.13)

для любого целого положительного k.

Аналогами интеграла непрерывной функции в пределах от 0 до t для решетчатой являются неполная сумма

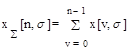(1.14)

и полная сумма

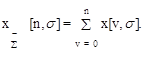(1.15)

Отличие (1.15) от (1.14) заключается в том, что значение x[n,s] в момент времени t = nT + sT также участвует в формировании результата.

Разностные уравнения (уравнения в конечных разностях) связывают между собой решетчатые функции и их конечные разности. При использовании прямых разностей неоднородные линейные разностные уравнения m-го порядка имеют вид [2]

b₀D^my[n,s] + b₁D^m-1y[n,s] + ... + b_m-1Dy[n,s] +b_my[n,s] = f[n,s], (1.16)

где f[n,s] - заданная, а y[n,s] - искомая решетчатые функции. При f[n,s] º 0 уравнение (1.16) становится однородным разностным уравнением, решением которого будет y[n,s].

При использовании (1.9) разностное уравнение (1.16) можно записать в другом виде:

a₀y[n+m,s] + a₁y[n+m-1,s] + ... + a_my[n,s] = f[n,s]. (1.17)

Коэффициенты этого уравнения определяются

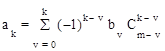, (1.18)

где биноминальные коэффициенты (число сочетаний)

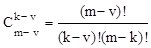. (1.19)

При использовании обратных разностей неоднородные линейные разностные уравнения m-го порядка будут

b₀Ñ^my[n,s] + b₁Ñ^m-1y[n,s] + ... + b_m-1Ñy[n,s] +b_my[n,s] = f[n,s]. (1.20)

С учетом (1.10) последнее выражение приобретает вид

a₀y[n,s] + a₁y[n-1,s] + ... + a_my[n-m,s] = f[n,s]. (1.21)

Коэффициенты этого уравнения определяются

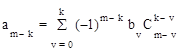, (1.22)

где биноминальные коэффициенты (число сочетаний)

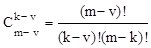. (1.23)

Разностные уравнения можно рассматривать как рекуррентные соотношения, позволяющие вычислять значения y[n+m,s] при n = 0, 1, 2, ... для уравнения (1.17) и заданных начальных значений y[0,s], y[1,s], ..., y[m-1,s] или значения y[n,s] при n = 0, 1, 2, ... для уравнения (1.21) и заданных начальных значений y[n-m,s], y[n-m+1,s], ..., y[n-1,s].

Решение уравнения (1.21) при s = 0 представляет собой рекуррентную формулу:

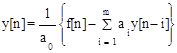, для n=0, 1, 2, ... (1.24)

при нулевых начальных условиях y[n] º 0 при n < 0. Структурная схема решения приведена на рис. 1.4.

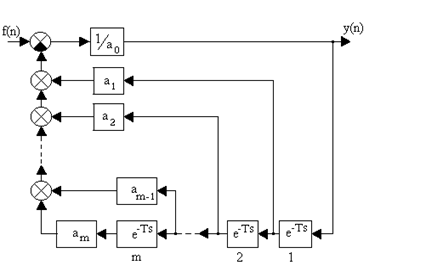Рис. 1.4.Структурная схема решения разностного уравнения

Общее решение однородного разностного уравнения при некратных корнях характеристического уравнения может быть записано следующим образом:

y[n,s] = 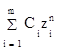, (1.25)

где z_i - корни характеристического уравнения

a₀ z^m + a₁z^m-1 + ... + a_m = 0, (1.26)

C_i - постоянные коэффициенты.

Для получения возможности исследования решений разностных уравнений в общем виде широко используются дискретное преобразование Лапласа, z-преобразование, w-преобразование, а также частотные методы.

Z - преобразование. Подобно тому, как применение преобразования Лапласа к линейным дифференциальным уравнениям дало возможность получить удобную методику анализа непрерывных систем, для дискретных систем также был разработан ряд специальных преобразований. Из них наибольшее распространение получили дискретное пребразование Лапласа, введенное в 1949 г. Я.З.Цыпкиным [18], и z-преобразование, предложенное в конце 40-х годов Штибицем и Шенноном.

Z-пребразованием решетчатой функции x[nT] называется функция комплексного аргумента z, определяемая выражением

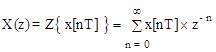(1.27)

при çzô>R=1/r , где r - радиус сходимости ряда.

Функция x[nT] называется оригиналом, а функция X(z) - изображением или z-пребразованием функции x[nT].

Преобразование, в котором z = e^sT, было введено Я.З.Цыпкиным под названием “дискретное преобразование Лапласа”.

Z-пребразование (1.27) дает возможность получить из X(z) значение ординат решетчатой функции x[nT] в моменты квантования. Но в системах управления с непрерывными динамическими частями процесс непрерывен и между моментами n = 0, 1, 2 ... Для нахождения этих ординат необходимо рассмотреть последовательности для других дискретных моментов с тем же интервалом повторения, но смещенных на значение sT: t = (n+s)T при 0 £ s £ 1. Это можно делать с помощью модифицированного z-преобразования.

Модифицированное z-преобразование решетчатой функции x[nT+sT]:

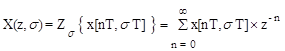. (1.28)

Функция X(z,s), определяемая выражением (1.28), называется z-преобразованием непрерывной функции времени x(t) и обозначается как

X(z,s) = Z_s {x(t)}; (1.29)

z-преобразование функции x(t) можно также представить следующим образом:

X(z,s) = Z_s {X(s)}, (1.30)

где X(s) - преобразование Лапласа от x(t). В этом случае подразумевается, что преобразованию подвергается функция времени и запись (1.30) носит чисто формальный характер.

Т а б л и ц а 1. 1