Условия устойчивости импульсных систем
| Степень характеристического уравнения | Условия устойчивости |
| m=1 | a0+a1>0, a0-a1>0 |
| m=2 | a0+a1+a2>0, a0-a1+a2>0, a0-a2>0 |
| m=3 и т.д. | a0+a1+a2+a3>0, a0-a1+a2-a3>0, a0(a0-a2)-a3(a3-a1)>0, 3(a0+a3)-a1-a3>0 |
Сложность условий устойчивости резко возрастает с ростом степени m характеристического полинома замкнутой системы. Поэтому практически алгебраический критерий используется при m £ 3.
Аналог критерия Михайлова. Для устойчивости линейной импульсной системы m-го порядка необходимо и достаточно, чтобы изменение аргумента функции D(e jwT) при изменении частоты w от 0 до p/T равнялось бы значению mp, то есть
D arg D (e jwT) = mp , 0 £ w £ p/T. (1.97)
Здесь D (e jwT) получается путем замены z на e jwT в характеристическом полиноме замкнутой импульсной системы
D(z) = a0zm + a1zm-1 + ... + am-1z + am , z = e jwT.
На рис. 1.14 приведены аналоги кривых Михайлова для устойчивой и неустойчивой импульсной системы при m = 3.
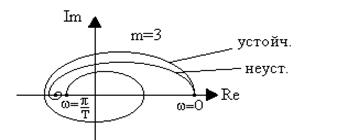
Рис. 1.14. Аналоги годографов Михайлова
Аналог критерия Найквиста. Если разомкнутая система устойчива, то для устойчивости замкнутой импульсной системы требуется, чтобы амплитудно-фазовая частотная характеристика разомкнутой импульсной системы W(ejwT) не охватывала точку с координатами (-1, j0 ). Для устойчивости замкнутой системы при неустойчивой разомкнутой цепи требуется, чтобы амплитудно-фазовая характеристика разомкнутой цепи охватывала точку (-1, j0) на угол pp (против часовой стрелки), где p - число полюсов разомкнутой цепи, лежащих вне единичного круга z = e jwT.
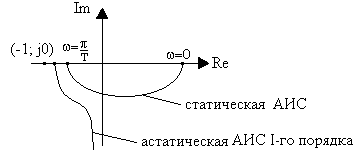
Рис. 1.15.АФЧХ устойчивых импульсных систем
На рис. 1.15 показаны амплитудно-фазовые частотные характеристики устойчивых импульсных систем.
Для пользования критериями устойчивости Гурвица и Михайлова в обычной формулировке отображают внутренность круга единичного радиуса плоскости z на левую полуплоскость комплексной переменной w (рис. 1.16) с помощью конформного преобразования [5]
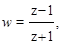
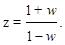 (1.98)
(1.98)
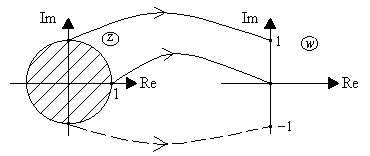
Рис. 1.16. Конформное преобразование
После подстановки z из (1.98) в (1.95) получим преобразованное характеристическое уравнение импульсной системы
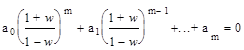 , (1.99)
, (1.99)
которое приводится к виду
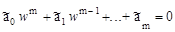 . (1.100)
. (1.100)
Все корни zi уравнения (1.95), лежащие внутри единичного круга, перейдут в левую полуплоскость w (рис. 1.16). Поэтому при использовании преобразованного характеристического уравнения (1.100) для устойчивости импульсной системы необходимо и достаточно, чтобы все корни wi (i = 1, 2, ..., m) имели отрицательные вещественные части. Границей устойчивости служит мнимая ось.
Для исследования устойчивости импульсных систем могут применяться также логарифмические частотные характеристики в той же формулировке, что и для обыкновенных линейных систем.
Дата добавления: 2015-06-01; просмотров: 1192;
