Переходный процесс
| Время t=nT | Выходная величина y[nT] |
| 1T 2T 3T 4T 5T 6T 7T и т.д. | 0.64 1.25 1.42 1.34 1.20 1.11 1.08 ... |
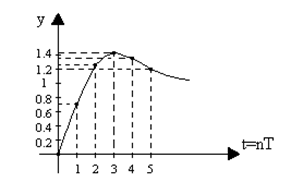
Рис. 1.17. График переходного процесса
Переходный процесс в импульсной системе может быть получен в результате решения разностного уравнения системы относительно дискретных значений входной g[nT] и выходной y[nT] координаты. Разностное уравнение определяется на основании дискретной передаточной функции замкнутой импульсной системы Ф(z) и имеет следующий вид (1.42)
a0y[n]+a1y[n-1]+...+amy[n-m]=b0g[n]+b1g[n-1]+...+blg[n-l], (1.103)
при m ³ l и y[n] º 0, f[n] º 0 для всех n < 0.
Решение его представляет собой рекуррентную формулу:
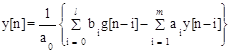; n=0, 1, 2, ... (1.104)
для нулевых начальных условий y[n] º 0 и g[n] º 0 при n < 0.
Формула (1.104) используется и для расчета переходных процессов в непрерывных системах после дискретизации их дифференциальных уравнений.
Дата добавления: 2015-06-01; просмотров: 967;