Переходные процессы в импульсных системах

Переходный процесс в импульсных системах определяется с помощью обратного z-преобразования, ряда Лорана, решения разностного уравнения, частотных методов, основанных на использовании вещественной или мнимой частотных характеристик замкнутой системы [9, 15, 17, 18].

Для расчета дискрет переходного процесса можно найти обратное z-преобразование изображения выходной величины системы y[n,s] = Z_s^-1{Y(z,s)}. При этом следует воспользоваться формулой обращения (1.41), которая устанавливает, что дискретные значения переходного процесса

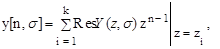(1.101)

где z_i - полюсы выражения Y(z,s); i = 1, 2, ..., k.

Вычет в простом полюсе определяется по формуле

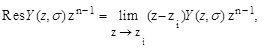
а в полюсе кратности r

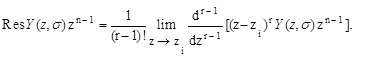
Дискретные значения переходного процесса могут быть найдены также путем разложения изображения выходной величины Y(z,s) в ряд Лорана по степеням z^-1

Y(z,s) = Y₀ + Y₁ z^-1 + Y₂ z^-2 + Y₃ z^-3 + ... . (1.102)

Коэффициенты этого ряда определяют значения выходной величины замкнутой импульсной системы в дискретные моменты времени t = (n+s)T. Так как изображение Y(z,s) представляет собой отношение двух полиномов, то коэффициенты ряда Y₀, Y₁, Y₂, ... могут быть получены делением полинома числителя на полином знаменателя. При малых периодах дискретности ряд сходится медленно и объем вычислительной работы значителен.

Пример. Определить переходный процесс при единичном ступенчатом входном воздействии на выходе импульсной системы, передаточная функция которой имеет следующий вид:

.

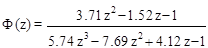Р е ш е н и е. Z-изображение входного воздействия G(z)=z/(z-1).

Следовательно, Y(z) = Ф(z)G(z) =

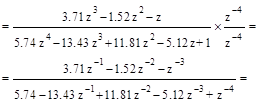
= 0.64z^-1+1.25z^-2+1.42z^-3+1.34z^-4+1.2z^-5+1.11z^-6+1.08z^-7+... .

Полученные коэффициенты сведены в табл. 1.3, на основании которой на рис. 1.17 построена кривая переходного процесса.

Т а б л и ц а 1. 3