Характеристики систем в пространстве состояний
Характеристики системы показывают ее принципиальные возможности. Эти возможности в значительной степени выявляются при изучении свойств системы, которые принято называть устойчивостью, наблюдаемостью, идентифицируемостью, управляемостью и адаптируемостью. Часто между наблюдаемостью и идентифицируемостью не делают различий, а адаптируемость рассматривается как частный случай управляемости.
Управляемость и наблюдаемость, так же как и устойчивость, относятся к числу важнейших характеристик динамических систем. Если устойчивость характеризует свойство системы возвращаться после возмущения в положение равновесия, то управляемость характеризует возможность изменения состояния системы с помощью входных сигналов, а наблюдаемость - возможность определения состояния системы по наблюдениям за ее выходными сигналами.
Устойчивость системы. Необходимым и достаточным условием устойчивости системы является отрицательность вещественных частей собственных чисел li матрицы А
Reli<0; i = 1, 2, ... , n, (10.25)
где li - корни характеристического уравнения çA-lEç= 0;
n - порядок системы.
Для того чтобы оценить расположение спектра матрицы A относительно мнимой оси, необходимо раскрыть характеристический определитель çA-lEç и получить характеристическое уравнение n-ой степени относительно l
çA-lEç= a0ln +a1ln-1 + a2ln-2 +...+ an-1l +an = 0. (10.26)
После получения характеристического уравнения в виде (10.26) обычно применяется тот или иной из известных критериев устойчивости, например, Рауса, Гурвица или Михайлова либо производится непосредственное вычисление всей совокупности корней, что в случае высокого порядка n матрицы A сопряжено со значительными трудностями и возможно лишь с помощью ЭВМ.
Кроме того, разработаны матричные критерии, позволяющие оценить устойчивость системы непосредственно по матрице A без нахождения характеристического полинома [14].
Для того чтобы система была асимптотически устойчива, необходимо и достаточно, чтобы для матрицы
G=E-2(E-A)-1
выполнялось условие
Gk®0, при k®¥. (10.27)
Выполнимость необходимого и достаточного условия устойчивости можно установить по факту абсолютного убывания элементов матрицы Gk. Возведение матрицы в степень рекомендуется выполнять так, чтобы каждая последующая матрица являлась квадратом предыдущей.
Управляемость системы. Система называется управляемой, если для любого начального состояния X(0)ÎRn существует управление U(t), переводящее ее за конечное время T в нулевое состояние X(T)=0 или система управляема, если существует управляющее воздействие U(t), позволяющее перевести ее за конечное время T в любое наперед заданное состояние из пространства состояний X(T)ÎRn.
Наблюдаемость системы. Система называется наблюдаемой, если по наблюдениям за выходным сигналом Y(t) в течение конечного времени T можно определить ее начальное состояние X(0).
Простые критерии проверки управляемости и наблюдаемости системы основаны на анализе матрицы управляемости
K=[B AB A2B ... An-1B] (10.28)
и матрицы наблюдаемости
L=[CT (CA)T (CA2)T ... (CAn-1)T]. (10.29)
Необходимым и достаточным условием управляемости системы является невырожденность матрицы управляемости
det K¹0, (10.30)
что эквивалентно условию равенства ранга матрицы К порядку n системы, то есть rank K = n. Если rank K < n, то система не полностью управляемая; если rank K = 0 - система полностью неуправляемая.
Необходимым и достаточным условием наблюдаемости системы является невырожденность матрицы наблюдаемости
det L¹0. (10.31)
что эквивалентно условию равенства ранга матрицы L порядку n системы, то есть rank L = n. Если rank L < n, то система не полностью наблюдаема.
Таким образом, управляемость системы определяется свойствами пары матриц A и B, а наблюдаемость - свойствами пары матриц A и C. Устойчивость системы определяется свойствами только одной матрицы A.
Пример. Оценить принципиальные возможности системы автоматического управления, заданной матрицами:
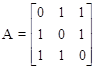 ,
,  ,
,  , D=[0].
, D=[0].
Решение. Характеристический определитель матрицы A
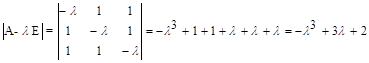 .
.
Решая уравнение  , находим собственные числа матрицы А: l1=2, l2 = -1, l3 = -1.
, находим собственные числа матрицы А: l1=2, l2 = -1, l3 = -1.
Система неустойчива, так как l1=2>0.
Матрица управляемости
 , det K=1-1=0, следовательно, система неуправляема.
, det K=1-1=0, следовательно, система неуправляема.
Матрица наблюдаемости
 , det L=1-1=0, следовательно, система ненаблюдаема.
, det L=1-1=0, следовательно, система ненаблюдаема.
Дата добавления: 2015-06-01; просмотров: 1892;
