Нормальная форма уравнений в пространстве состояний
Нормальная форма уравнений в пространстве состояний получается из стандартной формы (10.1) посредством преобразования подобия. При этом предполагается, что собственные числа матрицы А различные.
Введем линейное преобразование
X=MQ, (10.32)
где М - модальная матрица матрицы А.
Уравнения (10.1) перепишем
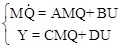 . (10.33)
. (10.33)
Умножив первое уравнение из (10.33) слева на М-1 , получим
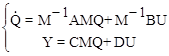 . (10.34)
. (10.34)
Так как M - модальная матрица, то
М-1АМ = L = 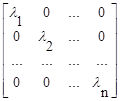 - диагональная матрица;
- диагональная матрица;
где li (при i = 1, 2, ... , n) - собственные числа матрицы А.
Следовательно, можно записать
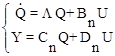 , (10.35)
, (10.35)
где L=М-1АМ, Вn= М-1B, Cn=CM, Dn=D - матрицы;
Q=[q1,q2,...,qn]T - вектор состояния системы, элементами которого являются новые переменные состояния qi (при i=1, 2, ... , n).
Система (10.35) представляет собой нормальную форму уравнений описания систем управления в пространстве состояний.
Нормальная форма уравнений состояния позволяет декомпозировать многосвязную систему n-го порядка на n взаимонесвязанных систем, при этом дифференциальные уравнения становятся развязанными относительно переменных состояния q1,q2,...,qn, т.е. они имеют вид
 , (10.36)
, (10.36)
где fi - внешнее воздействие на i-ю переменную состояния.
Таким образом, переход к нормальной форме существенно упрощает исследование многосвязных систем.
В случае кратных собственных чисел матрицы A диагональная матрица L заменяется матрицей J, которая строится из клеток Жордана, например,
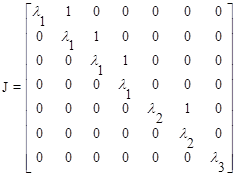 . (10.37)
. (10.37)
Таким образом, из сравнения уравнений (10.1) и (10.35) следует, что при математическом описании одного и того же динамического процесса различному выбору переменных состояния соответствуют различные матрицы системы, управления, наблюдения, связи и различные векторные дифференциальные уравнения, каждое из которых полностью определяет выходную величину системы.
Пример. Написать уравнения состояний в нормальной форме для динамической системы, представленной на рис.10.3.
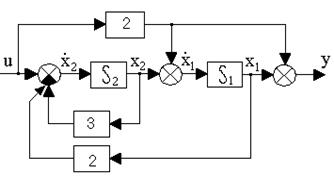
Рис. 10.3. Структурная схема системы в переменных состояния
Решение. Выберем в качестве переменных состояния системы сигналы на выходах интеграторов x1 и x2. В этом случае структурной схеме (рис.10.3) соответствует следующая система уравнений (стан-дартная форма)

Откуда матрицы
 ,
, 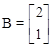 ,
, 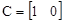 , D=[2].
, D=[2].
Собственные числа матрицы A: l1= -1, l2= -2.
Модальная матрица M= 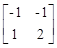 и M-1=
и M-1= 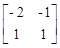 .
.
Тогда диагональная матрица системы, матрица управления, матрица наблюдения и матрица связи будут
L=  , Вn= М-1B=
, Вn= М-1B=  , Cn=CM=[-1 -1], Dn=D=[2].
, Cn=CM=[-1 -1], Dn=D=[2].
Отсюда получаем уравнения состояний системы в нормальной форме
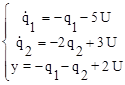 ,
,
которым соответствует структурная схема системы, приведенная на рис.10.4.

Рис. 10.4. Структурная схема системы в переменных состояния
по полюсам
Дата добавления: 2015-06-01; просмотров: 1260;
