Структура решения уравнений переменных состояния
Рассмотрим линейную однородную систему с постоянными коэффициентами [14]
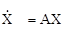. (10.8)
Решение ее X(t) характеризует свободное поведение системы. Пусть вектор начальных условий имеет вид
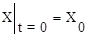. (10.9)
Разложим искомый вектор X(t) в степенной ряд по t:
. (10.10)
Дифференцируя (10.8), найдем
; 
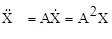и т.д. (10.11)
Тогда при t=0 получим
; 
; 
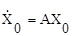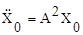и т.д. (10.12)
В итоге ряд (10.10) можно переписать в виде
(10.13)
Подставляя еАtX0 в исходное уравнение (10.8), легко убедиться, что (10.13) представляет собой решение. Полагая в (10.13) t=0, получим X0.
Таким образом, интегрирование однородной системы (10.8) сводится к вычислению матрицы еАt и умножению ее на вектор начальных условий X0. Матрица еАt называется матричным экспоненциалом или матричной экспонентой. В теории управления она часто называется переходной матрицей состояния.
Решение однородного уравнения (10.8) имеет вид
. (10.14)
Если движение начинается в момент времени t=t0, то решение принимает форму
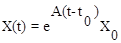. (10.15)
Матрица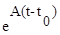 
может быть представлена в виде разложения в матричный степенной ряд
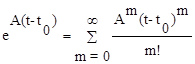, 10.16)
который сходится абсолютно и равномерно при любом значении t.
Основные свойства матрицы еАt :
1. Матрицы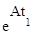 
и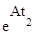 
коммутируют, то есть
. (10.17)
2. Матрица еАt - всегда неособенная, ее обратная матрица
(еАt )-1= е-At . (10.18)
3. Если АВ=ВА, то
е(A+B)= еА еВ= еВ еА . (10.19)
4. Производная еАt
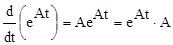. (10.20)
Это означает, что матрица еАt коммутирует с A.
5. Интеграл еАt
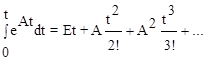, (10.21)
откуда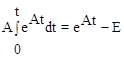 
.
Если матрица А - неособенная, получим
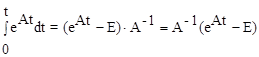. (10.22)
Для решения неоднородного уравнения преобразуем его к виду
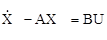
и умножим слева на е-At
.
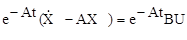Левая часть уравнения
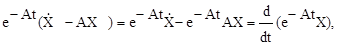
поскольку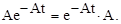 
Тогда
.
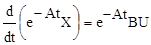Интегрирование последнего выражения дает
.
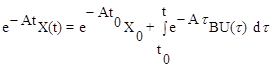Умножая полученное уравнение слева на еАt и учитывая свойство (10.18), получим окончательно
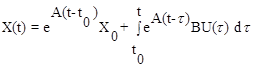. (10.23)
Первое слагаемое в (10.23) представляет собой решение однородного дифференциального матричного уравнения и описывает свободное движение системы, вызванное начальными условиями, второе слагаемое - вынужденное движение под влиянием внешнего воздействия U(t).
Тогда полное решение системы (10.1) имеет вид
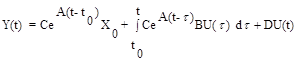. (10.24)
Дата добавления: 2015-06-01; просмотров: 1118;