Приложение 2. Решение системы дифференциальных уравнений.

Ниже приводится один из методов решения системы дифференциальных уравнений.

Рассмотрим систему, состоящую из одного ремонтируемого элемента и имеющую два состояния:

S₀(t) –– система в момент t находится в рабочем состоянии;

S₁(t) –– система в момент t находится в ремонте ( не работает).

Система уравнений Колмогорова имеет вид:

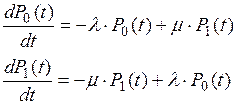(П2.1)
Найдем интеграл этой системы уравнений, для чего

введем обозначения P₀(t)=y, P₁(t)=z.

Тогда система уравнений принимает вид:

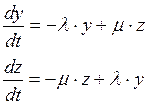(П2.2)
Дифференцируем первое уравнение:

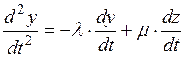(П2.3)
Из первого же уравнения находим z:

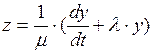(П2.4)
Из второго уравнения системы после подстановки найденного выражения для z имеем:

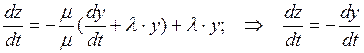(П2.5)
Подставляем полученное выражение производной (П2.5) в уравнение (П2.3), получим:

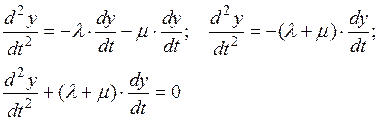(П2.6)
Характеристическое уравнение имеет вид:

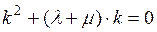(П2.7)
Решение характеристического уравнения дает корни:

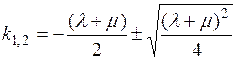, откуда

k₁=0, k₂=-(l+m) (П2.8)
Общее решение системы однородных дифференциальных уравнений при вещественных и неравных корнях имеет вид:

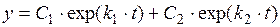, (П2.9)
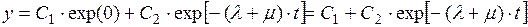(П2.10)

Учитывая начальные условия

y(0)=1 z(0)=0 (П2.11)
получим:

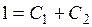(П2.12)
Тогда

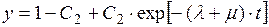(П2.13)
Дифференцируем (П2.10):

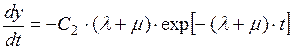(П2.14)
Подставляя в (П2.4) выражения (П2.13) и (П2.14), получим:

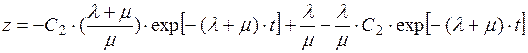(П2.15)

При подстановке начального условия z(0) = 0, получим уравнение:

,

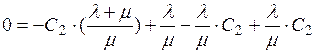откуда

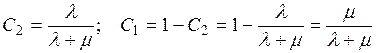(П2.16)
Подставляя (П2.16) в (П2.10) и (П2.15), получим окончательно:

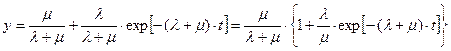(П2.17)
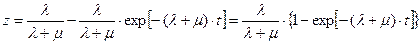(П2.18)

Заключение

Настоящее пособие составлено по материалам последних публикаций по теории надежности технических систем, в прикладном ее аспекте.

В отличие от предыдущего издания (2000 г.) в пособии исключены материалы, не вошедшие в курс лекций ни на факультете безопасности, ни на инженерно-строительном факультете Санкт-Петербургского государственного политехнического университета. Сокращено число задач, относящихся к проверке знаний по теории вероятностей, исключены задачи, связанные с расчетами параметров случайных функций.

Вместе с тем в пособие добавлен раздел логико-вероятностных методов оценки надежности (за что отдельное спасибо профессору Рябинину И.А.), без которых определение надежности систем сложных структур становится весьма затруднительной. Добавлены примеры оценки надежностной и структурной значимости элементов, входящих в состав сложных систем.

Решение многих примеров изменено с целью использования современных вычислительных средств персональных компьютеров, например, в разделе 7 приведено решение системы дифференциальных уравнений Колмогорова с помощью Mathcad, приведены графики изменения во времени вероятностей различных состояний системы.

Перечисленные выше изменения проведены с целью адаптации пособия к современным вычислительным средствам и приближения теории надежности технических систем к практическим задачам.