Некоторые свойства интегралов, зависящих от параметра.

Бета-функция (эйлеров интеграл 1-го рода).

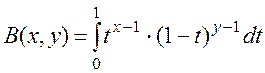(П1.20)
Интеграл (П1.20) сходится при x>0, y>0 и расходится, если нарушается хоть одно из этих неравенств.

Свойства бета-функции.

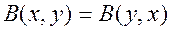
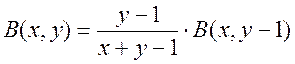
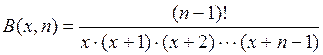при n = 1,2,…

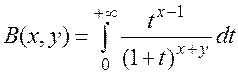
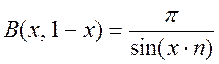при 0 < x < 1

Гамма-функция (эйлеров интеграл 2-го рода).

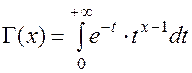(П1.21)

Этот несобственный интеграл сходится при x>0 и расходится

при x £ 0.

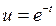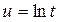Подстановкой и , получим соответственно:

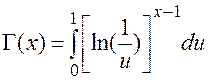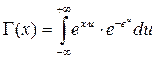; (П1.22)
Свойства гамма-функции.

При x>0 гамма-функция непрерывна и имеет непрерывные производные любого порядка:

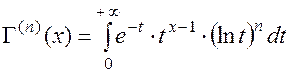
Представление Гаусса (в виде произведения):

,

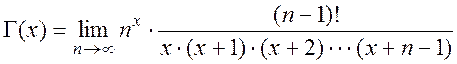при x>0.

Функциональное равенство:

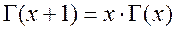
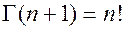при n=0, 1, 2, ….

Связь с бета-функцией:

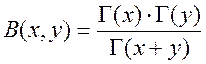
Закон дополнения:

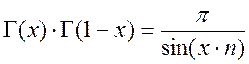при 0<x<1

Закон удвоения Лагранжа:

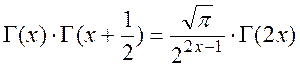
теорема умножения

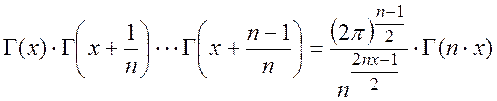
Формула Раабе:

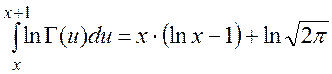
Формула Гаусса:

,

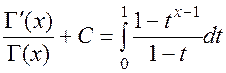где С–– постоянная Эйлера, С=0.577 215 664 901 532…

Формула Коши:

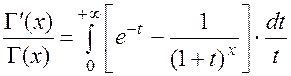
Использование гамма-распределения.

11.Интенсивность отказов

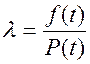(П1.23)
12. Плотность гамма-распределения

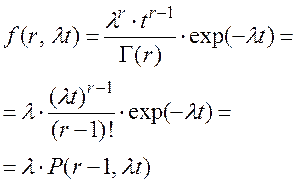(П1.24)
откуда вероятность того, что на интервале (0, t) не произойдет (r-1) отказ

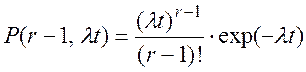(П1.25)

или

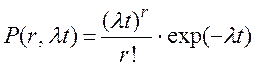(П1.26)
Некоторые полезные соотношения.

Вероятность того, что на интервале (0, t) произойдет ровно r отказов

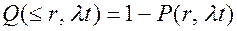(П1.27)
Вероятность того, что на интервале (0, t) произойдет не более r отказов

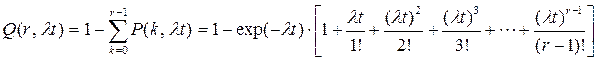
Вывод многих выражений для нормального закона распределения требует использования следующих интегралов:

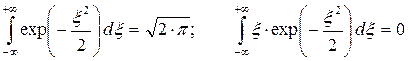(П1.28)
Некоторые простые, но полезные преобразования

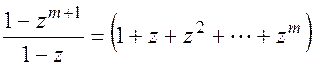(П1.29)

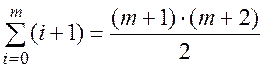(П1.30)

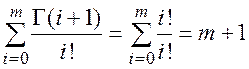(П1.31)

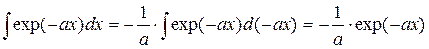(П1.32)

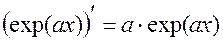(П1.33)

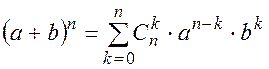
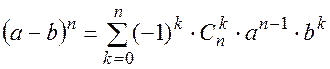
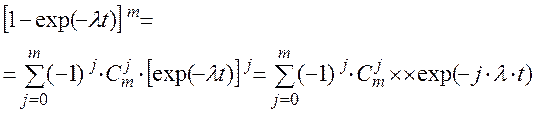(П1.34)

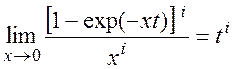(П1.34)