Приложение 1. Определения и свойства факториалов, перестановок, сочетаний.

Факториалом целого положительного числа n называется произведение:

n!=1×2×3×××(n-1)×n (П1.1)
По определению 0! = 1.

Свойства факториалов:

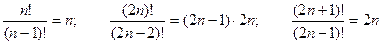(П1.2)
при возрастании n факториал n! растет очень быстро:

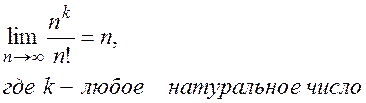(П1.3)

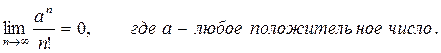(П1.4)
факториалы больших чисел можно приближенно оценить по формуле Стирлинга:

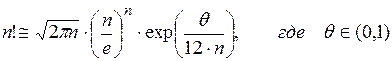(П1.5)
Перестановками из n элементов называют их группировки, отличающиеся друг от друга только порядком входящих в них элементов.

Например, перестановки из трех элементов a,b,c:

a,b,c; a,c,b; c,a,b; b,a,c; b,c,a; c,b,a.

Число всех различных перестановок из n различных элементов обозначают P_n и вычисляют по формуле:

P_n = 1×2×3×××(n-1)×n = n! (П1.6)
Сочетаниями из данных n элементов называют их всевозможные группировки по m элементов в каждой, отличающимися друг от друга хотя бы одним элементом.

Например, сочетания из четырех элементов a,b,c,d, по два элемента:

аb, ac, ad, bc, bd, cd.

Число всех сочетаний из n элементов по m обозначают :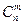

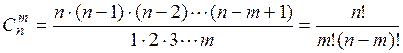, (П1.7)
Например,

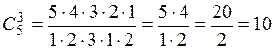
Свойства сочетаний:

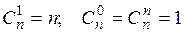(П1.8)

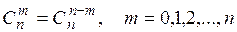(П1.9)

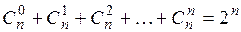(П1.10)

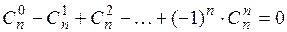(П1.11)
Разложение функций в ряд Тейлора.

Функция f(x) называется аналитической в точке х₀, если для всех х , удовлетворяющих условию 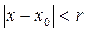(r>0), f(x) есть сумма некоторого степенного ряда:

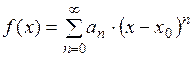
Если функция f(x) аналитична в точке х₀ , то в некоторой окрестности х₀ она дифференцируема любое число раз и:

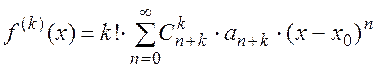, тогда

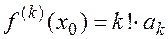(П1.12)

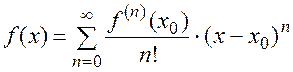(П1.13)

Разложение функций в ряд Тейлора позволяет получать удобные для вычисления формулы, например:

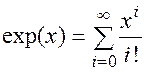(П1.14)

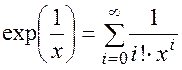(П1.15)

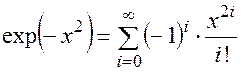(П1.16)

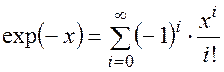(П1.17)

,

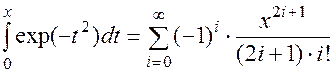для 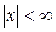(П1.18)

Разложение функций в ряд Тейлора можно использовать для оценки погрешности. Например, если система состоит из n элементов и ее надежность определяется произведением надежностей p_i каждого элемента, то абсолютная погрешность вычисления надежности Р_С системы может быть оценена по формуле (ограничиваясь первыми членами разложения):

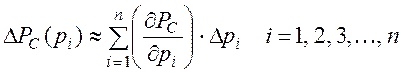(П1.19)
где 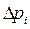–– может быть принята равной величине абсолютной погрешности числового значения p_i.