Системы массового обслуживания. Системой массового обслуживания (СМО) называется любая система, предназначенная для обслуживания какого-либо потока заявок.
Системой массового обслуживания (СМО) называется любая система, предназначенная для обслуживания какого-либо потока заявок.
СМО технических систем в интересах оценки их надежности делятся на системы с отказами в обслуживании (в ремонте) и системы с ожиданием обслуживания (ремонта). В первом случае заявка покидает систему (узел не ремонтируется), во втором –– ждет очереди ремонта.
Рассматриваются далее только системы, где потоки событий, производящие изменение состояния системы, являются пуассоновскими.
Работа СМО с отказами характеризуется следующими параметрами:
число каналов n;
плотность потока заявок l;
плотность потока обслуживаний одного канала m (плотность потока заявок, обслуживаемых одним постоянно занятым каналом).
Величина m обратна среднему времени обслуживания одной заявки:
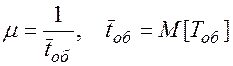(2.89)
где Тоб –– случайное время обслуживания.
Рассмотрим систему массового обслуживания, изменение состояний которой представлено на рис.2.7.10:
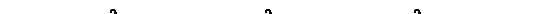
Рис. 2.7.10. Размеченный граф системы массового обслуживания с отказами.
Состояние Хк (0 £ к £ n) адекватно тому, что занято ровно к каналов из их общего числа n. При этом предполагается, что каждый канал может обслуживать только одну заявку, а каждая заявка обслуживается только одним каналом.
Или иначе. Состояние Хк –– занято обслуживанием к каналов, т.е. интенсивность обслуживания в к раз выше интенсивности обслуживания одним каналом (т.е. k×m). Поскольку рассматривается система с отказами, то более l интенсивность заявок быть не может (в противном случае число заявок составляло бы l×k, где k=1,2,…n).
Из приведенного на рис.2.7.10 графа следует система дифференциальных уравнений:
……………………………….
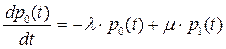
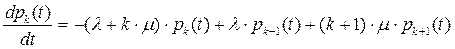(2.90)
………………………………
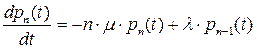
Эту систему обычно интегрируют при начальных условиях:
,
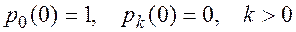(в начальный момент все каналы свободны).
При t ® ¥ существует предельный (установившейся) режим работы системы, при котором вероятности состояний определяются формулами Эрланга:
–– вероятность рк того, что в системе имеется ровно к заявок (0 £ k £ n), все они обслуживаются и очереди нет
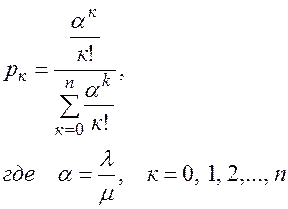(2.91)
–– вероятность робсл того, что заявка будет обслужена (не получит отказа) определяется соотношением (вероятность того, что хоть один канал будет свободен):
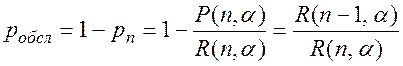(2.92)
где рn –– вероятность того, что заняты n каналов,
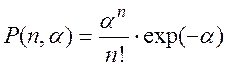(2.93)
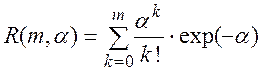(2.94)
Между функциями P(k,a) и R(k,a) существует связь:
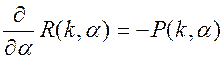(2.95)
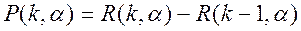(2.96)
Полезным представляется также знание предельных соотношений:
(2.97)
Последние соотношения имеют следующий смысл. Вероятность того, что случайная величина не превысит значения k®¥ равна единице, а вероятность того, что на элементарный временной интервал выпадет число событий k®¥ равна нулю.
Система массового обслуживания называется чистой системой с ожиданием, если ни время пребывания заявки в очереди, ни число заявок в очереди ничем не ограничено.
Если имеются ограничения по одному из этих признаков, то система называется системой смешанного типа.
Для СМО смешанного типа с ограничениями по числу мест в очереди предельные вероятности состояний выражаются ниже приведенными формулами (2.98), (2.99).
При этом ограничения по времени пребывания заявки в очереди при составлении уравнений для вероятностей состояний учитывается тем, что на каждую заявку, находящуюся в очереди, действует поток «уходов» с плотностью, обратной среднему времени пребывания заявки в очереди.
Вероятность того, что в системе смешанного типа с ограниченной «длиной очереди» m имеется k заявок и все заявки обслуживаются определяется формулой:
(2.98)
Вероятность того, что в системе все n каналов заняты и S заявок находятся в очереди определяется соотношением:
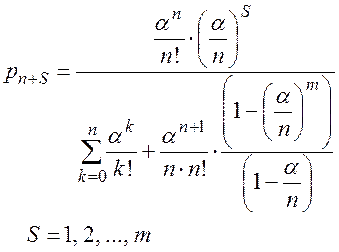(2.99)
где n –– число каналов обслуживания; m –– число мест в очереди;
l –– плотность потока заявок; m –– плотность потока обслуживания одного канала.
Примечание. Здесь S –– означает, что на S заявок очередь может превышать число каналов. Например, каналов 12, очередь 17, а предельное значение длины очереди 21 заявка (m=21), тогда, поскольку очередь меньше предельного значения длины (17<21), то S=17-12=5.
Для чистой системы с ожиданием (m = ¥) установившийся (предельный) режим существует только в случае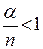 
. Предельные вероятности при этом равны:
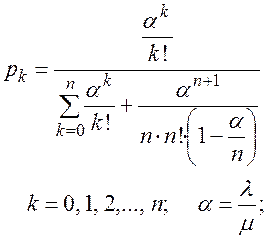(2.100)
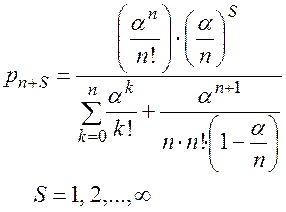(2.101)
Приведенные соотношения могут быть представлены в несколько ином виде. Введем обозначение:
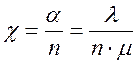
Тогда, для систем смешанного типа, когда число мест в очереди ограничено (m = const):
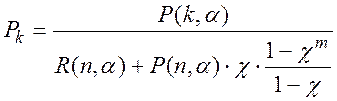(2.102)
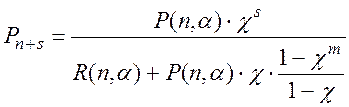(2.103)
Вероятность обслуживания в этом случае может быть представлена в виде:
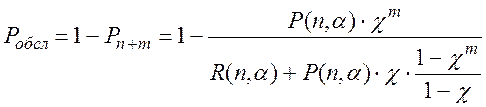(2.104)
Для чистой системы с ожиданием установившийся предельный режим существует при c<1, тогда:
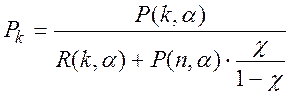(2.105)
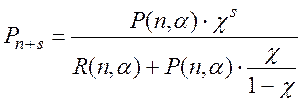(2.106)
Математическое ожидание числа заявок, находящихся в очереди (длины очереди):
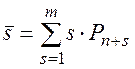(2.107)
Дата добавления: 2015-05-26; просмотров: 987;