Задача 2.35.
Техническое устройство состоит из n узлов. Каждый узел может выходить из строя независимо от других. Узлы выходят из строя только последовательно, по одному. Время исправной работы i-го узла распределено по показательному закону с параметром li :
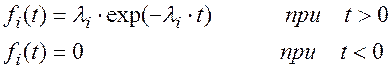
Каждый узел, оказавшийся неисправным, немедленно заменяется новым и поступает в ремонт. Ремонт узлов производится последовательно, по одному. Ремонт i-го узла продолжается случайное время, распределенное по показательному закону с параметром mi:
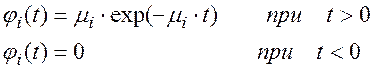
Устройство работает в течение времени t.
Требуется определить:
а. Математическое ожидание и дисперсию числа узлов, подлежащих замене.
б. Математическое ожидание суммарного времени Т, которое будет затрачено на ремонт вышедших из строя узлов.
Решение.
а. Обозначим через Xi число узлов i-го типа, вышедших из строя за время t. Очевидно, что эта случайная величина распределена по закону Пуассона и имеет:
математическое ожидание 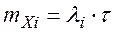
дисперсию 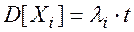 .
.
Обозначим через Х общее число узлов, вышедших из строя за время t. Тогда имеем:
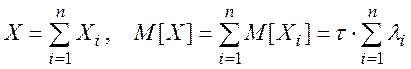
Поскольку величины Хi независимы, то:
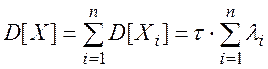
б. Обозначим через Тi общее время, затраченное на ремонт всех вышедших из строя за время t узлов i-го типа. Оно представляет собой сумму времен, затраченных на ремонт каждого из узлов. Поскольку число вышедших из строя узлов i-го типа равно Xi , имеем:
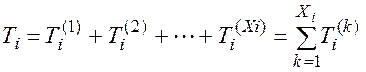 ,
,
где 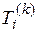 –– случайная величина, распределенная по показательному закону с параметром mi.
–– случайная величина, распределенная по показательному закону с параметром mi.
Величины 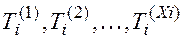 –– независимы.
–– независимы.
Найдем математическое ожидание величины Тi. Для этого вначале предположим, что случайная величина Xi приняла определенной значение, тогда:
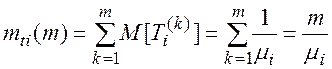
Умножив это условноематематическое ожидание на вероятность Pm того, что случайная величина Xi приняла значение m, и просуммировав все эти произведения, мы найдем полное (безусловное) математическое ожидание величины Тi:
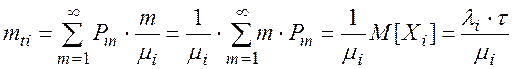
Применяя далее теорему сложения математических ожиданий, получим:
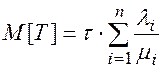
Замечание.
Тот же результат можно получить путем следующих (не вполне строгих) рассуждений. Среднее число выходов из строя узлов i-го типа за время t равно li×t. Среднее время ремонта одного узла i-го типа равно 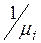 , а среднее время, которое будет затрачено на ремонт всех вышедших за время t узлов i-го типа равно
, а среднее время, которое будет затрачено на ремонт всех вышедших за время t узлов i-го типа равно 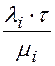 . Тогда среднее время, которое будет затрачено на ремонт узлов всех типов будет равно:
. Тогда среднее время, которое будет затрачено на ремонт узлов всех типов будет равно: 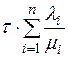 .
.
Марковские процессы, потоки событий. Элементы теории массового обслуживания.
Говорят, что в физической системе происходит случайный процесс, если она с течением времени может под влиянием случайных факторов переходить из состояния в состояние.
Потоком событий называется последовательность событий, наступающих одно за другим в случайные моменты времени.
Плотностью (интенсивностью) потока называется среднее число событий в единицу времени.
Большое значение имеют процессы, для которых состояние системы изменяется в случайные моменты времени. Особую роль играют такого рода процессы, для которых выполнены три условия:
стационарность,
отсутствие последействия,
ординарность.
Процессы, удовлетворяющие всем этим условиям, называются простейшими или однородными процессами Пуассона.
В перечисленные условия вкладывается следующий смысл.
Стационарность означает, что для любой группы из конечного числа непересекающихся промежутков времени вероятность наступления определенного числа событий на протяжении каждого из них зависит от этих чисел и от длительности промежутков времени, но не зависит от сдвига всех временных отрезков на одну и ту же величину. В частности, вероятность появления m событий в течение промежутка от t до t +Dt не зависит от t и является функцией только m, Dt.
Отсутствие последействия означает, что вероятность наступления m событий в течение интервала времени (t, t+Dt) не зависит от того, сколько раз и как появились события ранее. Это предположение означает, что условная вероятность появления m событий на промежутке (t, t+Dt) при любом предположении о наступлении событий до момента t совпадает с безусловной вероятностью. Отсутствие последействия означает взаимную независимость появления того или иного числа событий в непересекающиеся моменты времени.
Ординарность выражает собой требование практической невозможности появления двух и более событий за малый промежуток времени Dt. Точнее, это означает следующее: обозначим через 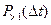 вероятность появления более, чем одного события за этот малый промежуток времени. Тогда условие ординарности состоит в следующем:
вероятность появления более, чем одного события за этот малый промежуток времени. Тогда условие ординарности состоит в следующем:
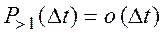
Если Pk(t) –– вероятность появления ровно k событий за время t:
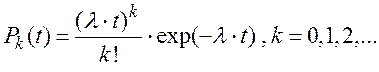
то P0(t) –– можно интерпретировать как вероятность того, что длительность промежутка времени между двумя последовательными появлениями событий окажется большей t.
Если события образуют пуассоновский поток, то число m событий, попадающих на любой интервал времени (t0, t0+t) распределено по закону Пуассона:
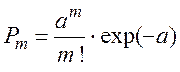 (2.74)
(2.74)
где a –– математическое ожидание числа событий, попадающих на этот участок:
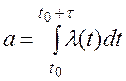 (2.75)
(2.75)
l(t) –– плотность (интенсивность) потока.
Если l(t)=const , пуассоновский поток называется стационарным пуассоновским или простейшим потоком.
Расстояние (временной интервал) Т между двумя соседними событиями в простейшем потоке есть непрерывная величина, распределенная по показательному закону с плотностью:

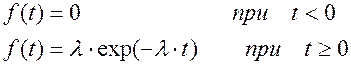 (2.76)
(2.76)
Для случайной величины Т, распределенной по показательному закону, справедливы характеристики:
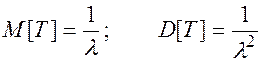 (2.77)
(2.77)
В физической системе S происходит случайный процесс, если она с течением времени может под влиянием случайных факторов изменять свое состояние.
Случайный процесс, протекающий в системе, называется процессом с дискретным временем, если переходы системы из состояния в состояние возможны только в определенные моменты времени t1, t2,…tn,… Если переходы возможны в любые произвольные моменты времени, процесс называется процессом с непрерывном временем.
Случайный процесс с дискретным состоянием называется марковским, если все вероятностные характеристики в будущем зависят только от того, в каком состоянии находится этот процесс в настоящее время и не зависят от того, каким образом этот процесс протекал в прошлом. Будущее зависит от прошлого только через настоящее. Если процесс марковский, то все потоки событий, переводящие систему из состояния в состояние, являются пуассоновскими.
При анализе случайных процессов с дискретным состоянием удобно пользоваться геометрической схемой, называемой графом состояний, который изображает возможные состояния системы и возможные переходы из состояния в состояние.
Каждое состояние системы обозначается квадратом или кружком, а возможные переходы системы из состояния в состояние –– стрелками, соединяющими квадраты или кружки. Заметим (рис. 2.7.1), что стрелками отмечаются только непосредственные переходы системы из состояния в состояние.
Например, если система из состояния S0 может перейти в состояние S3 только через состояние S1 или S2 , то стрелками отмечаются только переходы из S0 в S1 и из S0 в S2, а не из состояния S0 в S3.
Рис. 2.7.1. Граф состояний системы.
В теории надежности чаще встречаются ситуации, когда переходы системы из состояния в состояние происходят в случайные моменты времени, которые заранее предсказать невозможно. Для описания таких процессов в ряде случаев может быть применена схема марковского процесса с дискретным состоянием и непрерывным временем.
Система S называется системой с дискретным состоянием, если она имеет счетное множество возможных состояний (число состояний можно перенумеровать) S1, S2,…,Sn,… и переход из одного состояния в другое осуществляется скачком. В дальнейшем рассматриваются только системы с дискретным состоянием.
Состояние системы называется «состоянием без выхода», если из него невозможен переход ни в какое другое состояние.
Для описания случайного процесса, протекающего в системе, зачастую пользуются вероятностями состояний:
p1(t), p2(t),…,pn(t),
где pk(t) –– вероятность того, что в момент t система находится в состоянии Sк.
Вероятности pk(t) удовлетворяют условию:
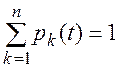
Введем в рассмотрение плотность lij вероятностей перехода системы из состояния Si в состояние Sj.

Рис. 2.7.2. Представление режима работы системы во времени.
Пусть система (рис.2.7.2.) в момент t находится в состоянии Si. Рассмотрим элементарный участок Dt, примыкающий к моменту t.
Назовем плотностью вероятностей (или интенсивностью) перехода из состояния Si в состояние Sj величину lij как предел отношения вероятности перехода от состояния Si в состояние Sj за время Dt к продолжительности этого промежутка времени Dt:
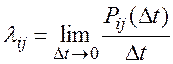 (2.78)
(2.78)
где Pij(Dt) –– вероятность того, что система, находившаяся в момент t в состоянии Si , за время Dt перейдет в состояние Sj (справедливо только для i¹j).
При малом значении временного интервала Dt вероятность Pij(Dt) с точностью до бесконечно малых высшего порядка малости равна:
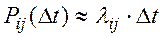 (2.79)
(2.79)
Если все интенсивности перехода lij не зависят от времени, марковский процесс называют однородным, в противном случае –– процесс называется неоднородным.
Пусть нам известны все lij для всех пар (Si, Sj) . Построим граф состояний системы и против каждой стрелки поставим соответствующую плотность вероятности перехода (рис. 2.7.3). Такой граф называется размеченным графом состояний.

Рис.2.7.3. Пример построения размеченного графа.
При наличии размеченного графа состояний системы, можно определить вероятности состояний P0(t), P1(t), P2(t)…как функции времени, а именно, эти вероятности удовлетворяют дифференциальным уравнениям Колмогорова.
Продемонстрируем методику вывода системы дифференциальных уравнений Колмогорова на конкретном примере (рис.2.7.4).
Пусть система имеет пять состояний S0, S1, S2, S3, S4. Поставим задачу найти одну из вероятностей состояния, например, P0(t). Это есть вероятность того, что в момент t система будет находиться в состоянии S0.
Придадим моменту t малое приращение Dt и найдем вероятность того, что в момент t+Dt система будет находиться в состоянии S0.
Реализация такого события возможна двумя путями:
а) система не изменит своего состояния за промежуток времени Dt;
б) система, находясь в момент t в состоянии S3, перейдет за Dt в состояние S0.
Вариант а)реализуется, если в момент t система с вероятностью P0(t) находилась в состоянии S0 и не перешла из состояния S0 в состояние S1. Вероятность последнего события может быть вычислена (для малых значений Dt) по формуле:
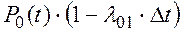 ,
,
где P0(t) –– вероятность нахождения системы в момент t в состоянии S0, l01×Dt –– вероятность перехода системы за промежуток времени Dt из состояния S0 в состояние S1, (1-l01×Dt) –– вероятность неперехода системы за интервал времени Dt из состояния S0 в состояние S1.

Рис. 2.7.4. Фрагмент размеченного графа технической системы.
Вариант б)реализуется в том случае, если система в момент t находилась с вероятностью Р3(t) в состоянии S3 и за интервал времени Dt перешла в состояние S0:
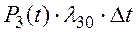 ,
,
где l30×Dt –– вероятность перехода за малый интервал времени Dt системы из состояния S3 в состояние S0.
Поскольку система в момент t+Dt могла находиться в состоянии Р0 только или первым или вторым способом, то получаем:
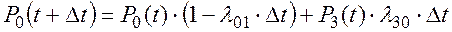
откуда:
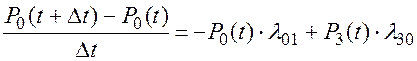 (2.80)
(2.80)
или:
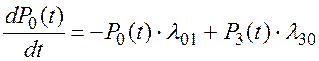 (2.81)
(2.81)
Рассмотрим состояние S1 и выведем уравнение для определения вероятности P1(t) того, что в момент t+Dt система будет находиться в состоянии S1.
Реализация такого состояния возможна, если:
система находилась в момент t в состоянии S0 и за время Dt перешла в состояние S1. Вероятность такого перехода определяется произведением соответствующих вероятностей:
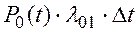
система в момент t находилась в состоянии S1 и за интервал Dt своего состояния не изменила, т.е. не перешла ни в состояние S2, ни в состояние S3. Оценим вероятность осуществления этого варианта.
Вероятность того, что система, находясь в состоянии S1, перейдет за время Dt в состояние S2 или S3:
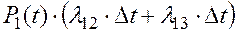
Вероятность неперехода системы из состояния S1 ни в одно из этих состояний:
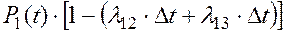
Окончательно получим:
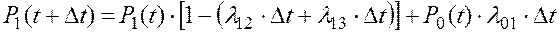
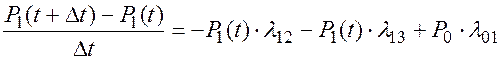
Или, при стремлении Dt к нулю, имеем окончательно:
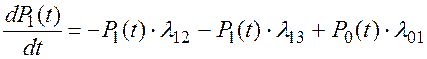 (2.82)
(2.82)
Аналогичным образом могут быть получены зависимости системы дифференциальных уравнений Колмогорова для всех остальных состояний рассматриваемой системы.
В итоге получим систему дифференциальных уравнений:

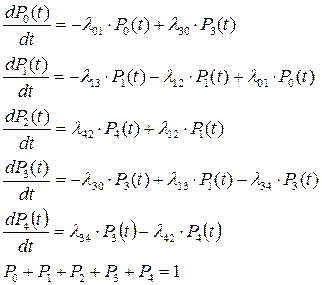 (2.83)
(2.83)
Интегрирование этой системы дифференциальных уравнений при начальных, условиях, например,
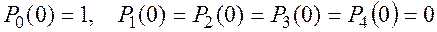
дает искомые функции вероятностей состояний: 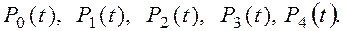
Все уравнения (2.83) построены по определенному правилу, зная которое можно выписывать систему для размеченного графа почти автоматически:
в левой части каждого уравнения стоит производная 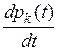 ,
,
в правой части содержится столько членов, сколько стрелок связано непосредственно с данным k –– м состоянием,
член правой части уравнения имеет знак плюс, если стрелка ведет в данное состояние и знак минус,если стрелка выходит из данного состояния,
каждый член правой части уравнения равен плотности потока событий, переводящего системупо данной стрелке, умноженной на вероятность того состояния, изкоторого исходит стрелка.
Эти правила составления системы дифференциальных уравнений Колмогорова справедливы для любой непрерывной марковской цепи.
Например.

Рис. 2.7.5. Размеченный граф системы с дискретным состоянием
и непрерывным временем.
Система дифференциальных уравнений такой системы имеет вид:

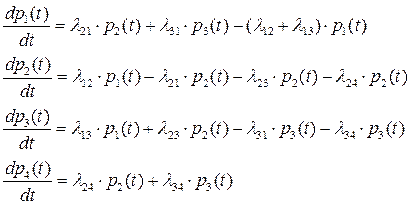 (2.84)
(2.84)
Начальные условия для интегрирования такой системы отражают состояние системы в начальный момент времени. Так, если в момент t=0 система была в состоянии Sk , то полагают:
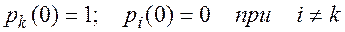
Число уравнений в системе может быть уменьшено на единицу, если учесть условие, что для любого t (для рассматриваемой системы):
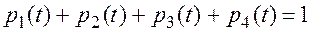
Дата добавления: 2015-05-26; просмотров: 1015;
