Задача 2.33.
При работе прибора возникают случайные неисправности. Среднее число неисправностей, возникающих в единицу времени работы прибора, равно l. Число неисправностей за время t работы прибора –– случайная величина, распределенная по закону Пуассона с параметром а=l×t. Для ликвидации возникшей неисправности (ремонта) требуется случайное время Трем . Это время ремонта распределено по показательному закону:
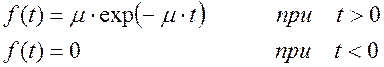
Времена устранения неисправностей неизвестны.
Найти:
а) среднюю долю времени, которую прибор будет исправно работать, и среднюю долю времени, которую он будет находиться в ремонте;
б) средний интервал времени между двумя последовательными неисправностями.
Решение.
Среднее время исправной работы (математическое ожидание времени, которое проработает прибор после пуска до остановки для ремонта) равно:
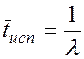
Среднее время ремонта:
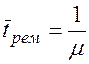
Средняя доля a времени, которую прибор будет работать исправно:
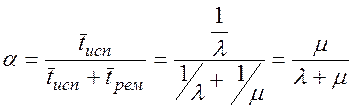
Средняя доля b времени, которую прибор будет находиться в ремонте:
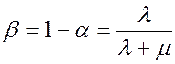
Средний интервал времени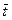 
между двумя последовательными неисправностями определяется по теореме сложения математических ожиданий (математическое ожидание суммы случайных величин равно сумме их математических ожиданий):
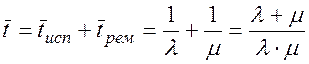
Дата добавления: 2015-05-26; просмотров: 717;