Предельные вероятности состояний.

Пусть имеется техническая система с дискретными состояниями, в которой протекают марковские случайные процессы с непрерывным временем. Предположим, что все интенсивности потоков событий, переводящие систему из состояния в состояние постоянны, т.е. все потоки событий –– простейшие (стационарные пуассоновские).

Сформулируем следующую задачу: что будет происходить с системой при стремлении t ® ¥ ? Если функции P_i(t) будут стремиться к каким-либо пределам, то будем их называть предельными вероятностями состояний.

Можно доказать следующее общее положение.

Если число состояний системы конечно и из каждого состояния за конечное число шагов можно перейти в любое другое (замкнутая система, рис.2.8а), то предельные вероятности состояний существуют и они не зависят ни от времени, ни от начального состояния системы.

При этом, естественно, сохраняется условие:

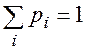(2.85)

Рис. 2.7.8 а) –– граф замкнутой системы

Рис. 2.7.8 б) –– граф разомкнутой системы

Таким образом, при t ® ¥ в системе устанавливается некоторый предельный стационарный режим, который состоит в том, что система случайным образом меняет свои состояния, но вероятность каждого из них уже не зависит от времени: каждое из состояний реализуется с некоторой постоянной вероятностью P_i.

При этом предельная вероятность P_i представляет собой среднее относительное время пребывания системы в данном i-м состоянии, т.е. после перехода системы в установившийся режим работы она будет находиться в состоянии S_i в течение времени, пропорциональном P_i.

Например, если система имеет состояния S₀, S₁, S₂ и предельные вероятности равны 0.4, 0.1, 0.5, то после перехода в установившийся режим 40% времени система будет находиться в состоянии S₀, 10% –– в состоянии S₁ и 50% –– в состоянии S₂.

Для вычисления предельных вероятностей в системе дифференциальных уравнений Колмогорова необходимо левые части уравнений положить равными нулю (как производные от постоянных, поскольку теперь вероятности состояний не зависят от времени). Тогда исходная система дифференциальных уравнений трансформируется в систему линейных алгебраических уравнений, решение которых совместно с (2.85) дает возможность определить предельные вероятности P_i.

Размеченный граф замкнутой системы имеет следующий вид.

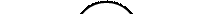
Рис. 2.7.9. Размеченный граф замкнутой системы.

Система дифференциальных уравнений Колмогорова:

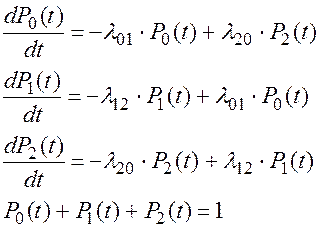(2.86)

Соответствующая линейная система алгебраических уравнений:

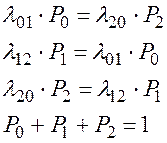(2.87)

Решением этой системы будут значения предельных вероятностей:

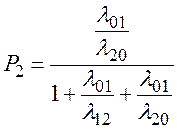(2.88)